CUPED方差缩减
对于成熟的产品来说,大多数的改动带来的提升可能都是微小的, 通常情况下,为提升AB实验的灵敏度,提升AB的显著性,有两种常见做法:
- 增加流量
- 增长实验时间
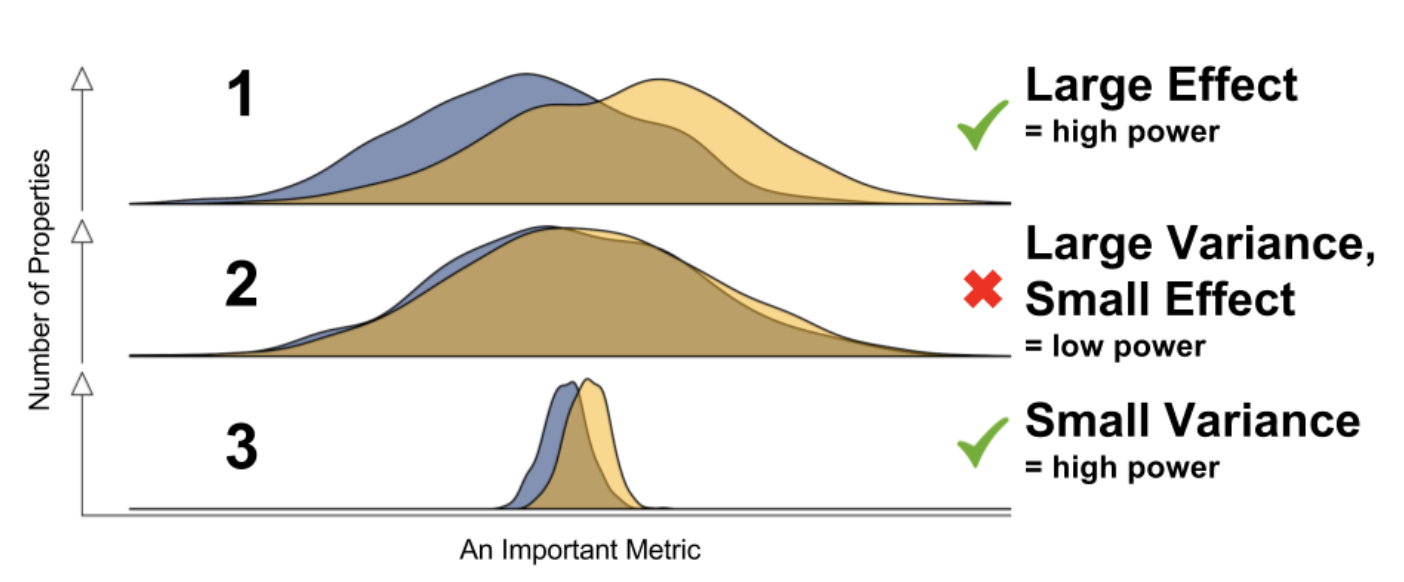
本质上,无论是延长实验时间还是增加流量一方面都是为了增加样本量,因为样本越多,方差越小,p值越显著,越容易检测出一些微小的改进。
如果能合理的通过统计方法降低方差,就可能更快,更少的样本的检测到微小的效果提升!
微软2013年发表过一篇论文,介绍了一种利用实验前的数据来缩减指标方差,进而提高实验灵敏度的方法,这种方法就是本文要介绍的CUPED(Controlled-experiment Using Pre-Experiment Data)。
CUPED算法
论文的核心在于通过实验前数据对实验核心指标进行修正,在保证无偏的情况下,得到方差更低, 更敏感的新指标,再对新指标进行统计检验(p值)。
这种方法的合理性在于,实验前核心指标的方差是已知的,且和实验本身无关的,因此合理的移除指标本身的方差不会影响估计效果。
作者给出了$Stratification$和$Covariate$两种方式来修正指标,同时给出了在实际应用中可能碰到的一些问题以及解决方法。
Stratifiaction
这种方式针对离散变量,一句话概括就是分组算指标。如果已知实验核心指标的方差很大,那么可以把样本分成K组,然后分组估计指标。这样分组估计的指标只保留了组内方差,从而剔除了组间方差。 $$ \begin{aligned} \hat{Y}_{strat}& =\sum_{k=1}^Kw_k*(\frac1{n_k}*\sum_{x_i\in k}Y_i) \\ Var(\hat{Y})& =Var_\text{within strat}+Var_\text{between strat} \\ &=\sum_{k=1}^K\frac{w_k}n\sigma_k^2+\sum_{k=1}^K\frac{w_k}n(\mu_k-\mu)^2 \\ &>=\sum_{k=1}^K\frac{w_k}n\sigma_k^2=Var(\hat{Y}_{strat}) \end{aligned} $$
Covariate
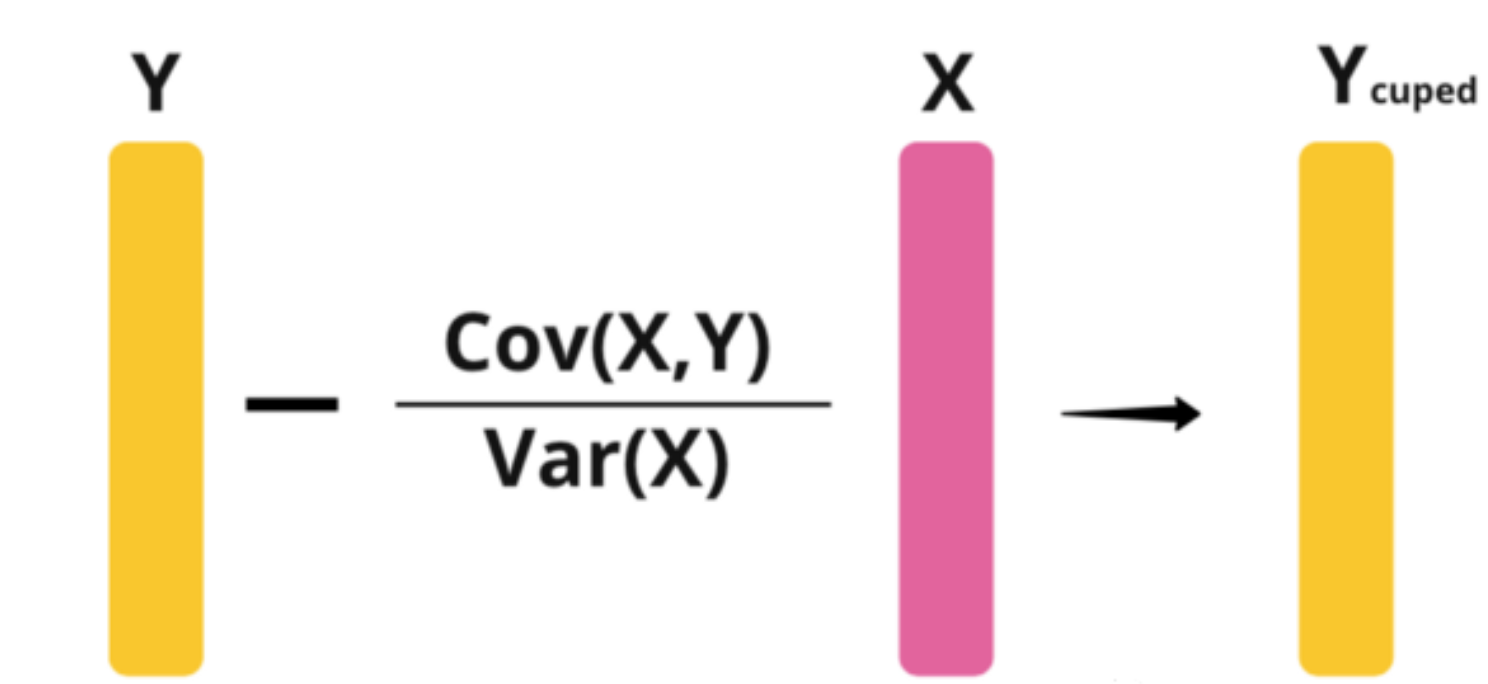
Covariate适用于连续变量。需要寻找和实验核心指标(Y)存在高相关性的另一连续特征(X),然后用该特征调整实验后的核心指标。X和Y相关性越高方差下降幅度越大。因此往往可以直接选择实验前的核心指标作为特征。只要保证特征未受到实验影响,在随机AB分组的条件下用该指标调整后的核心指标依旧是无偏的。
$$ \begin{aligned} Y_{i}^{cov}& =Y_i-\theta(X_i-E(X)) \\ \theta& =cov(X,Y)/var(X) \\ \end{aligned} $$
原始方差和缩减之后的方差关系: $$ Var(Y_{cov}) =Var(Y)*(1-\rho^2) \\ $$
$where~\rho = cor(Y, X)~is~the~correlation~between~Y~and~X$
covariate的选择
这里的选择包括两个方面,特征的选择和计算特征的$pre-experiment$时间长度的选择。
核心指标$X$在$pre-experiment$的估计通常是很好的covariate的选择,且估计covariate选择的时间段相对越长效果越好。时间越长covariate的覆盖量越大,且受到短期波动的影响越小估计更稳定。
需要注意的,不论你选择什么特征,都要保证: $$ E(X^{treatment})=E(X^{control}) $$ 即一定要保证所选的这个变量不会受实验策略的影响。比如用户首次进入实验的所属当天星期几就可以作为一个协变量。
没有pre-experiment数据怎么办
这个现象在互联网中很常见,新用户或者很久不活跃的用户都会面临没有近期行为特征的问题。作者认为可以结合$stratification$方法对有/无covariate的用户进一步打上标签。或者其实不仅局限于$pre-experiment$特征,只要保证特征不受到实验影响$post-experiment$特征也是可以的。
而在Booking的案例中,作者选择对这部分样本不作处理,因为通常缺失值是用样本均值来填充,在上述式子中就等于是不做处理。
Demo:
1import pandas as pd
2import numpy as np
3import hvplot.pandas
4from scipy.stats import pearsonr
5from scipy.optimize import minimize
6
7
8def generate_data(treatment_effect, size):
9 # generate y from a normal distribution
10 df = pd.DataFrame({'y': np.random.normal(loc=0, scale=1, size=size)})
11 # create a covariate that's corrected with y
12 df['x'] = minimize(
13 lambda x:
14 abs(0.95 - pearsonr(df.y, x)[0]),
15 np.random.rand(len(df.y))).x
16 # random assign rows to two groups 0 and 1
17 df['group'] = np.random.randint(0,2, df.shape[0])
18 # for treatment group add a treatment effect
19 df.loc[df["group"] == 1, 'y'] += treatment_effect
20 return df
21
22df = generate_data(treatment_effect=1, size=10000)
23theta = df.cov()['x']['y'] / df.cov()['x']['x']
24df['y_cuped'] = df.y - theta * df.x
25
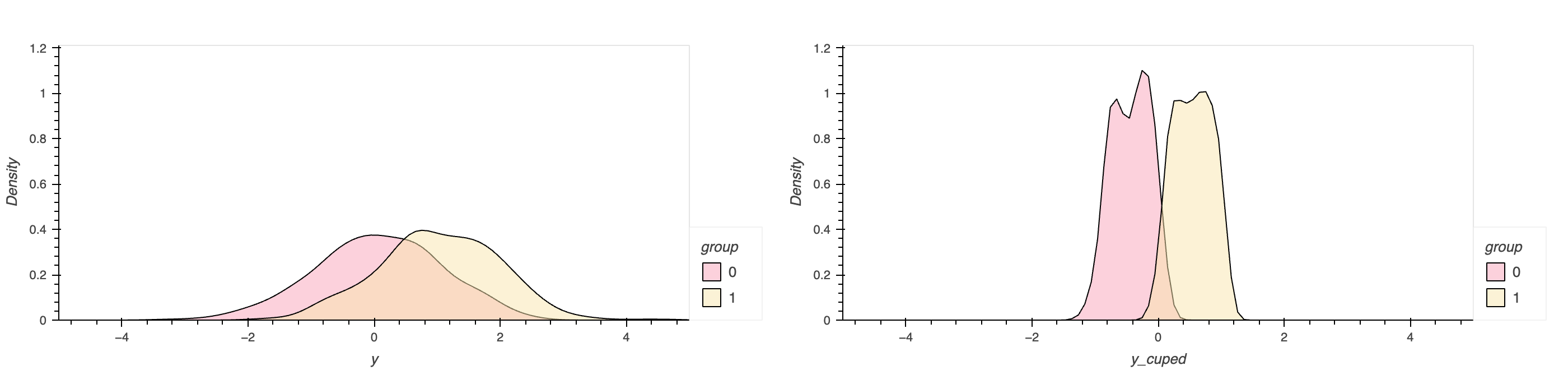
26# cuped前后的分布图
27(
28 df.hvplot.kde('y', by='group', xlim = [-5,5], color=['#F9a4ba', '#f8e5ad'])
29 + df.hvplot.kde('y_cuped', by='group', xlim = [-5,5], color=['#F9a4ba', '#f8e5ad'])
30)