Beta分布和Thompson采样
$Beta$分布
$Beta$分布是一个定义在[0,1]区间上的连续概率分布族,它有两个正值参数,称为形状参数,一般用$\alpha$和$\beta$表示
$Beta$分布的概率密度为: $$ f(x ; \alpha, \beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_{0}^{1} u^{\alpha-1}(1-u)^{\beta-1} d u}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1}=\frac{1}{B(\alpha, \beta)} x^{\alpha-1}(1-x)^{\beta-1} $$ 随机变量$X$服从参数为$\alpha, \beta$的$beta$分布,一般记作: $$ X \sim \operatorname {Beta} (\alpha, \beta) $$ $Beta$分布的期望: $$ \frac{\alpha}{\alpha + \beta} $$ $Beta$分布的方差: $$ \frac{\alpha \beta}{(\alpha+\beta)^{2}(\alpha+\beta+1)} $$ $Beta$分布的概率密度图:
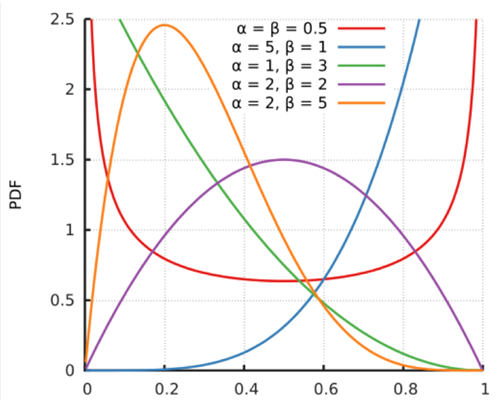
从$Beta$分布的概率密度函数的图形我们可以看出,$Beta$分布有很多种形状,但都是在$0~1$区间内,因此$Beta$分布可以描述各种$0~1$区间内的形状(事件)。因此,它特别适合为某件事发生或者成功的概率建模。同时,当$α=1,β=1$的时候,它就是一个均匀分布。
1from scipy.stats import beta
2import matplotlib.pyplot as plt
3import numpy as np
4
5x = np.linspace(0, 1, 100)
6
7a_array = [1, 2, 4, 8]
8b_array = [1, 2, 4, 8]
9
10for i, a in enumerate(a_array):
11 for j, b in enumerate(b_array):
12 plt.plot(x, beta.pdf(x, a, b), lw=1, alpha=0.6, label='a='+str(a)+',b='+str(b))
13
14plt.legend(frameon=False)
15plt.show()
贝塔分布主要有 $α$和 $β$两个参数,这两个参数决定了分布的形状,从上图及其均值和方差的公式可以看出:
-
$α/(α+β)$也就是均值,其越大,概率密度分布的中心位置越靠近1,依据此概率分布产生的随机数也多说都靠近1,反之则都靠近0。
-
$α+β$越大,则分布越窄,也就是集中度越高,这样产生的随机数更接近中心位置,从方差公式上也能看出来。
案例
$Beta$分布可以看作是一个概率的概率分布(如硬币正面朝上的概率的分布),当我们不知道一个东西的具体概率是多少时,它给出了所有概率出现的可能性大小,可以理解为概率的概率分布–贝叶斯的思维。
以棒球为例子:
熟悉棒球运动的都知道有一个指标就是棒球击球率(batting average),就是用一个运动员击中的球数除以击球的总数,我们一般认为0.266是正常水平的击球率,而如果击球率高达0.3就被认为是非常优秀的。
现在有一个棒球运动员,我们希望能够预测他在这一赛季中的棒球击球率是多少。你可能就会直接计算棒球击球率,用击中的数除以击球数,但是如果这个棒球运动员只打了一次,而且还命中了,那么他就击球率就是100%了,这显然是不合理的,因为根据棒球的历史信息,我们知道这个击球率应该是0.215到0.36之间才对啊。
对于这个问题,我们可以用一个二项分布表示(一系列成功或失败),一个最好的方法来表示这些经验(在统计中称为先验信息)就是用beta分布,这表示在我们没有看到这个运动员打球之前,我们就有了一个大概的范围。beta分布的定义域是(0,1)这就跟概率的范围是一样的。
接下来我们将这些先验信息转换为beta分布的参数,我们知道一个击球率应该是平均0.27左右,而他的范围是0.21到0.35,那么根据这个信息,我们可以取$α=81,β=219$
之所以取这两个参数是因为:
- beta分布的均值是$\frac{\alpha}{\alpha+\beta}=\frac{81}{81+219}=0.27$
- 从图中可以看到这个分布主要落在了$(0.2,0.35)$间,这是从经验中得出的合理的范围
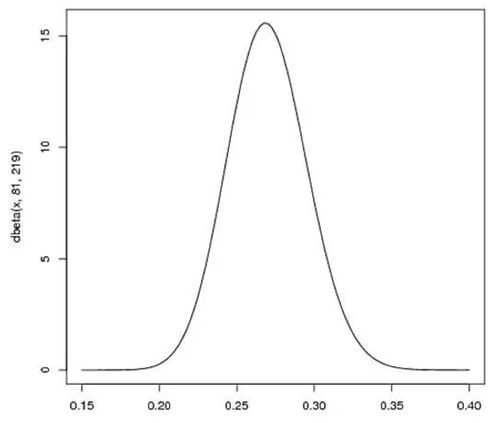
在这个例子里,我们的x轴就表示各个击球率的取值,x对应的y值就是这个击球率所对应的概率。也就是说beta分布可以看作一个概率的概率分布。
那么有了先验信息后,现在我们考虑一个运动员只打一次球,那么他现在的数据就是1中-1击。这时候我们就可以更新我们的分布了,让这个曲线做一些移动去适应我们的新信息。beta分布在数学上就给我们提供了这一性质,他与二项分布是共轭先验的。所谓共轭先验就是先验分布是beta分布,而后验分布同样是beta分布。结果很简单:
$$
\operatorname{Beta}\left(\alpha_{0}+\text { hits }, \beta_{0}+\text { misses }\right)
$$
如果我们得到了更多的数据,假设一共打了300次,其中击中了100次,200次没击中,那么这一新分布就是:$\operatorname{beta}(81+100,219+200)$
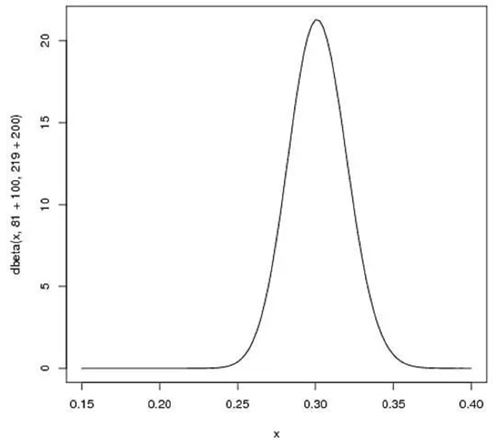
可以看出,曲线更窄而且往右移动了(击球率更高),由此我们对于运动员的击球率有了更好的了解。新的贝塔分布的期望值为0.303,比直接计算$100/(100+200)=0.333$要低,是比赛季开始时的预计0.27要高,所以贝塔分布能够抛出掉一些偶然因素,比直接计算击球率更能客观反映球员的击球水平。
$Beta$分布和二项分布
二项分布
$$ P(\text {data} \mid \theta) \propto \theta^{z}(1-\theta)^{N-z} $$
贝叶斯定理
$$ P(\theta \mid d a t a)=\frac{P(d a t a \mid \theta) P(\theta)}{P(d a t a)} \propto P(d a t a \mid \theta) P(\theta) $$
$P(\theta)$为$beta$分布时: $$ P(\theta) = \operatorname{Beta}(a, b)=\frac{\theta^{a-1}(1-\theta)^{b-1}}{B(a, b)} \propto \theta^{a-1}(1-\theta)^{b-1} $$ 则此时的后验分布为: $$ \begin{array}{c} P(\theta \mid d a t a) \propto \theta^{z}(1-\theta)^{N-z} * \theta^{a-1}(1-\theta)^{b-1} \ \propto \theta^{a+z-1}(1-\theta)^{b+N-z-1} \end{array} $$ 令$a′=a+z,b′=b+N−z$: $$ P(\theta \mid \text { data })=\frac{\theta^{a^{\prime}-1}(1-\theta)^{b^{\prime}-1}}{B\left(a^{\prime}, b^{\prime}\right)} $$ 可见,后验分布依然是一个$Beta$分布。所以,我们将$Beta$分布和二项分布称之为共轭分布
$Thompson$采样
$Thompson$采样的背后原理正是上述所讲的$Beta$分布,将$Beta$分布的 $\alpha$参数看成是推荐后用户点击的次数,把分布的 $\beta$ 参数看成是推荐后用户未点击的次数,则汤普森采样过程如下:
- 取出每一个候选对应的参数 a 和 b;
- 为每个候选用 a 和 b 作为参数,用贝塔分布产生一个随机数;
- 按照随机数排序,输出最大值对应的候选;
- 观察用户反馈,如果用户点击则将对应候选的 a 加 1,否则 b 加 1;
$Thompson$采样为什么有效呢?
-
如果一个候选被选中的次数很多,也就是 $a+b$ 很大了,它的分布会很窄,换句话说这个候选的收益已经非常确定了,就是说不管分布中心接近0还是1都几乎比较确定了。用它产生随机数,基本上就在中心位置附近,接近平均收益。
-
如果一个候选不但 a+b 很大,即分布很窄,而且 $a/(a+b) $也很大,接近 1,那就确定这是个好的候选项,平均收益很好,每次选择很占优势,就进入利用阶段。反之则有可能平均分布比较接近与0,几乎再无出头之日。
-
如果一个候选的 $a+b$ 很小,分布很宽,也就是没有被选择太多次,说明这个候选是好是坏还不太确定,那么分布就是跳跃的,这次可能好,下次就可能坏,也就是还有机会存在,没有完全抛弃。那么用它产生随机数就有可能得到一个较大的随机数,在排序时被优先输出,这就起到了前面说的探索作用。
代码实现:
1choice = numpy.argmax(pymc.rbeta(1 + self.wins, 1 + self.trials - self.wins))