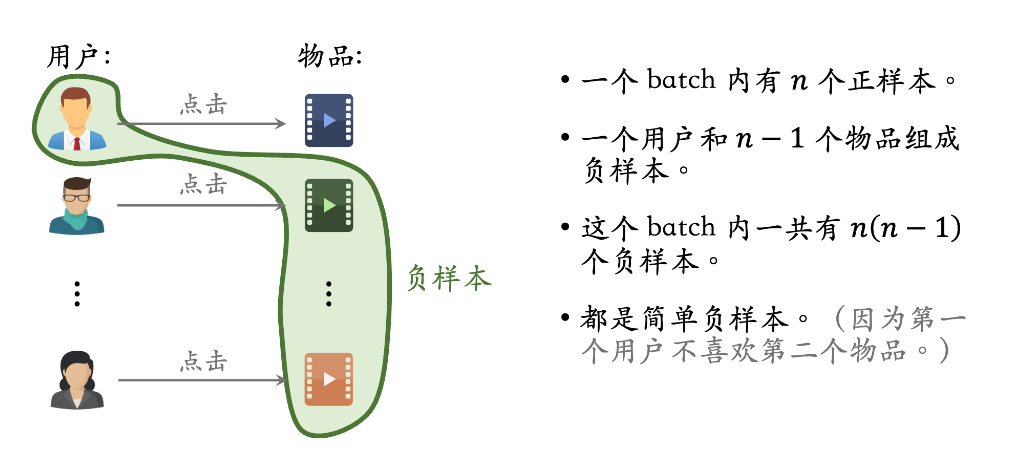
Batch内负采样
In-batch Negative Sampling
- code:
1import torch
2import torch.nn as nn
3import torch.nn.functional as F
4
5class RecommenderModel(nn.Module):
6 def __init__(self, user_size, item_size, embedding_dim):
7 super(RecommenderModel, self).__init__()
8 self.user_embedding = nn.Embedding(user_size, embedding_dim)
9 self.item_embedding = nn.Embedding(item_size, embedding_dim)
10
11 def forward(self, user_ids, item_ids):
12 user_embeds = self.user_embedding(user_ids)
13 item_embeds = self.item_embedding(item_ids)
14 return user_embeds, item_embeds
15
16 def in_batch_negative_sampling_loss(user_embeds, item_embeds):
17 batch_size = user_embeds.size(0)
18
19 # 正样本得分 (batch_size,)
20 positive_scores = torch.sum(user_embeds * item_embeds, dim=-1)
21
22 # 负样本得分 (batch_size, batch_size)
23 negative_scores = torch.matmul(user_embeds, item_embeds.t())
24
25 # 创建标签 (batch_size, batch_size)
26 labels = torch.eye(batch_size).to(user_embeds.device)
27
28 # 计算损失
29 loss = F.cross_entropy(negative_scores, labels.argmax(dim=-1))
30
31 return loss
32
33# 示例数据
34batch_size = 4
35embedding_dim = 8
36user_size = 100
37item_size = 1000
38
39user_ids = torch.randint(0, user_size, (batch_size,))
40item_ids = torch.randint(0, item_size, (batch_size,))
41
42model = RecommenderModel(user_size, item_size, embedding_dim)
43user_embeds, item_embeds = model(user_ids, item_ids)
44
45loss = in_batch_negative_sampling_loss(user_embeds, item_embeds)
46print(f'Loss: {loss.item()}')
优点
- 效性:批量内负采样能够充分利用每个训练批次中的样本,提高训练效率,避免显式生成大量负样本的开销。
- 适用性:这种方法特别适用于深度学习的推荐系统,在大规模数据训练时效果显著。
- 实现:通过在每个批次中将其他正样本视为负样本,并使用合适的损失函数(如交叉熵损失),可以有效地优化模型。
缺点
- 对热门商品的打压过于严重

batch内的item对于当前user都是正样本,这种样本天然要比随机采样的item的热度要高。也就是说,我们采样了一批热门商品当作负样本(hard negtive-sample)。这样难免对于热门商品的打压太过了,可以在计算<user, item>得分时,减去商品的热度,来补偿。

sampled_softmax loss
$$\mathcal{L}=-log{\left[\frac{exp(s_{i,i}-log(p_j))}{\sum_{k\neq i}exp(s_{i,k}-log(p_k))+exp(s_{i,i} - log(p_i))}\right]}$$
对每个item j,假设被采样的概率为$p_j$,那么$log Q$矫正就是在本来的内积上加上 $-log{p_j}$ $$ s^c(x_i, y_j) = s(x_i, y_j) – \log {p_j} $$
$p_j$的概率通过距离上一次看到y的间隔来估计,item越热门,训练过程中就越经常看到item,那么距离上次看到y的间隔B(y)跟概率p成反比。于是有如下算法

在实践当中,对每个y都可以用PS的1维向量来存储对应的step,那么下一次再看到y时就可以计算出对应的间隔和概率了。
1step = get_global_step() # 获取当前的batch计数tensor
2item_step = get_item_step_vector() # 获取用于存储item上次见过的step的向量
3item_step.set_gradient(grad=step - item_step, lr=1.0)
4delta = tf.clip_by_value(step - item_step, 1, 1000)
5logq = tf.stop_gradient(tf.log(delta))
6batch_logits += logq # batch_logits 是前面计算的logits
7...
$$ \begin{aligned} \frac{\partial\mathcal{L}}{\partial {s_{i,j}}} \\ &=\frac{\exp(s_{i,j}-log(p_j))}{\sum_{j \neq i}\exp(s_{i,j}-log(p_j))+\exp(s_{i,i}-log(p_i))} \\ &=\frac1{p_j}P_{i,j} \end{aligned} $$
可以看到,越热门的负样本,${1} / {p_j}$越小,gradient越小,可以起到一定的补偿机制。
1def sampled_softmax_loss(weights,
2 biases,
3 labels,
4 inputs,
5 num_sampled,
6 num_classes,
7 num_true=1):
8 """
9 weights: 待优化的矩阵,形状[num_classes, dim]。可以理解为所有item embedding矩阵,那时 num_classes = 所有item的个数
10 biases: 待优化变量,[num_classes]。每个item还有自己的bias,与user无关,代表自己本身的受欢迎程度。
11 labels: 正例的item ids,形状是[batch_size,num_true]的正数矩阵。每个元素代表一个用户点击过的一个item id,允许一个用户可以点击过至多num_true个item。
12 inputs: 输入的[batch_size, dim]矩阵,可以认为是user embedding
13 num_sampled:整个batch要采集多少负样本
14 num_classes: 在u2i中,可以理解成所有item的个数
15 num_true: 一条样本中有几个正例,一般就是1
16 """
17 # logits: [batch_size, num_true + num_sampled]的float矩阵
18 # labels: 与logits相同形状,如果num_true=1的话,每行就是[1,0,0,...,0]的形式
19 logits, labels = _compute_sampled_logits(
20 weights=weights,
21 biases=biases,
22 labels=labels,
23 inputs=inputs,
24 num_sampled=num_sampled,
25 num_classes=num_classes,
26 num_true=num_true,
27 sampled_values=sampled_values,
28 subtract_log_q=True,
29 remove_accidental_hits=remove_accidental_hits,
30 partition_strategy=partition_strategy,
31 name=name,
32 seed=seed)
33 labels = array_ops.stop_gradient(labels, name="labels_stop_gradient")
34
35 # sampled_losses:形状与logits相同,也是[batch_size, num_true + num_sampled]
36 # 一行样本包含num_true个正例和num_sampled个负例
37 # 所以一行样本也有num_true + num_sampled个sigmoid loss
38
39 sampled_losses = sigmoid_cross_entropy_with_logits(
40 labels=labels,
41 logits=logits,
42 name="sampled_losses")
43
44 # We sum out true and sampled losses.
45 return _sum_rows(sampled_losses)
46
47def _compute_sampled_logits(weights,
48 biases,
49 labels,
50 inputs,
51 num_sampled,
52 num_classes,
53 num_true=1,
54 ......
55 subtract_log_q=True,
56 remove_accidental_hits=False,......):
57 """
58 输入:
59 weights: 待优化的矩阵,形状[num_classes, dim]。可以理解为所有item embedding矩阵,那时num_classes=所有item的个数
60 biases: 待优化变量,[num_classes]。每个item还有自己的bias,与user无关,代表自己的受欢迎程度。
61 labels: 正例的item ids,形状是[batch_size,num_true]的正数矩阵。每个元素代表一个用户点击过的一个item id。允许一个用户可以点击过多个item。
62 inputs: 输入的[batch_size, dim]矩阵,可以认为是user embedding
63 num_sampled:整个batch要采集多少负样本
64 num_classes: 在u2i中,可以理解成所有item的个数
65 num_true: 一条样本中有几个正例,一般就是1
66 subtract_log_q:是否要对匹配度,进行修正
67 remove_accidental_hits:如果采样到的某个负例,恰好等于正例,是否要补救
68 Output:
69 out_logits: [batch_size, num_true + num_sampled]
70 out_labels: 与`out_logits`同形状
71 """