多兴趣召回推荐
传统双塔
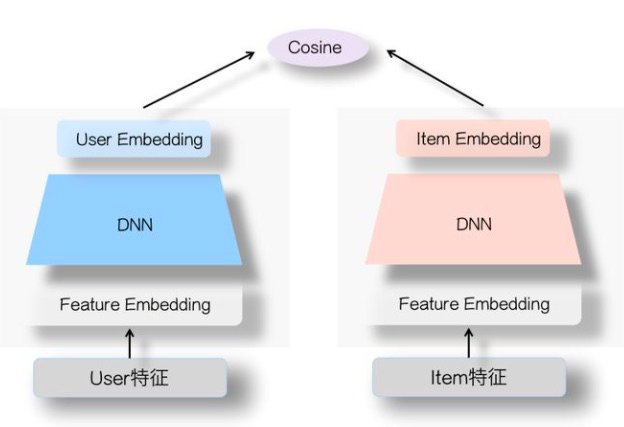
- user_tower: 产生$V_u$
- item_tower: 产生$V_i$
$$ score = f(u\_emb, i\_emb)= <V_u, V_i> $$
多兴趣双塔
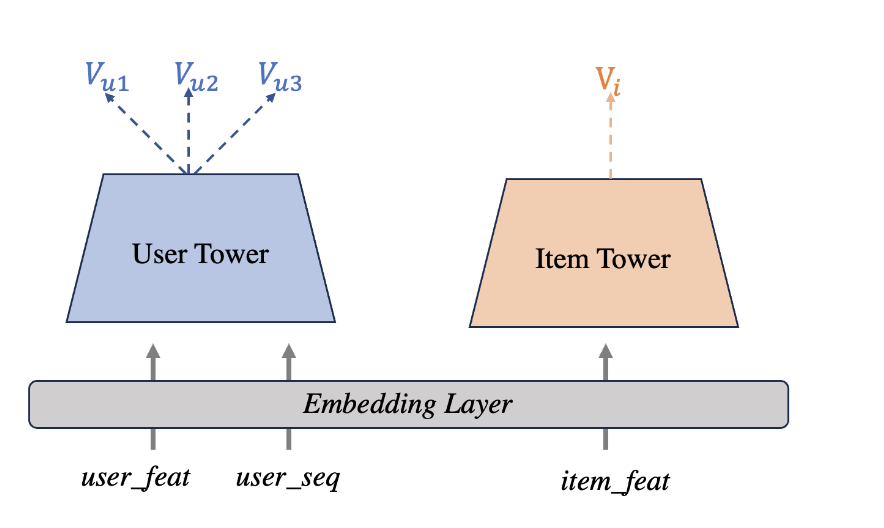
MIND
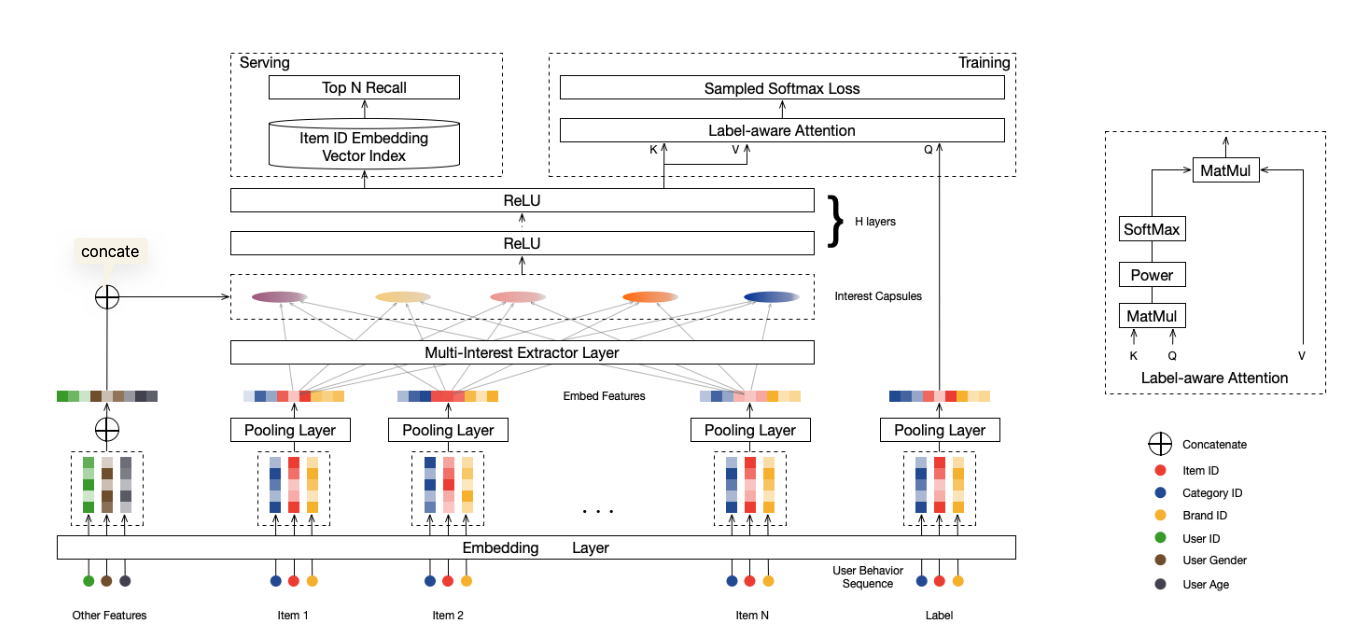
1interest_capsules = CapsuleLayer(input_units=user_seq_embedding.shape[-1],
2 out_units=params['embedding_dim'],
3 max_len=params['max_seq_len'],
4 k_max=params['k_max'],
5 mode=mode)((user_seq_embedding, like_user_seq_len)) # [B, k_max, embedding_dim]
6
7q_embedding_layer = tf.tile(tf.expand_dims(q_embedding, -2), [1, params['k_max'], 1]) # [B, k_max, 64]
8
9q_deep_input = tf.concat([q_embedding_layer, interest_capsules], axis=-1) # [B, k_max, embedding_dim+64]
$Dynamic \ \ Routing$:
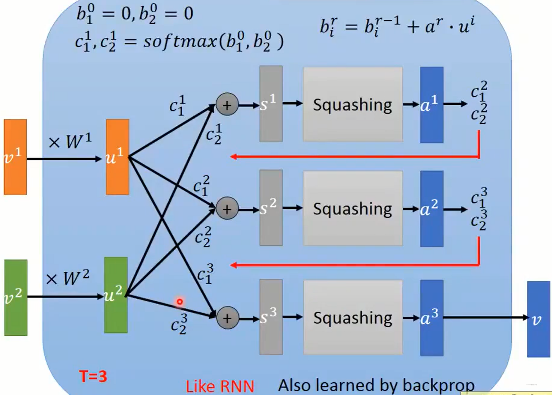
$Loss$:
$$ \begin{aligned} \overrightarrow{\boldsymbol{\upsilon}}_{u} &=\mathrm{Attention}\left(\overrightarrow{\boldsymbol{e}}_{i},\mathrm{V}_{u},\mathrm{V}_{u}\right) \\ &=\mathrm{V}_{u}\mathrm{softmax}(\mathrm{pow}(\mathrm{V}_{u}^{\mathrm{T}}\overrightarrow{\boldsymbol{e}}_{i},p)) \end{aligned} $$
问题
interest之间差异比较小,学到的兴趣接近
- 改进$squash$函数
$$
\text{squash函数: }a\leftarrow\frac{|a|^2}{1+|a|^2}\frac a{|a|} \\
\text{ 改进的Squash: }a\leftarrow pow\left(\frac{|a|^2}{1+|a|^2},\mathbf{p}\right)\frac a{|a|} \ \
(0 \leq p \leq 1) $$ - 或者对学到的K个兴趣向量加正则损失: $$ D_{output}=-\frac{1}{K^2}\sum_{i=1}^K\sum_{j=1}^K\frac{O^i\cdot O^j}{|O^i||O^j|} $$
ComiRec
$Dynamic \ \ Routing$提取兴趣

$Attention$机制提取兴趣
$$ \mathbf{A}=\mathrm{softmax}(\mathbf{W}_{2}^{\top}\tanh(\mathbf{W}_{1}\mathbf{H}))^{\top} \\ \mathbf{V}_{u}=\mathbf{HA} $$
- $\mathrm{H}\in \mathbb{R}^{d \times n}$ $\mathrm{where~}n\mathrm{~is~the~length~of~user~sequence}$
- $\mathbf{V}_{u}=[\mathbf{v}_{1},…,\mathbf{v}_{K}]\in\mathbb{R}^{d\times K}$ : $K个user \ \ emb$
$Loss$:
$$ \mathbf{v}_u=\mathbf{V}_u[:,\mathrm{argmax}(\mathbf{V}_u^\top\mathbf{e}_i)], \\ P_\theta(i|u)=\frac{\exp(\mathbf{v}_u^\top\mathbf{e}_i)}{\sum_{k\in I}\exp(\mathbf{v}_u^\top\mathbf{e}_k)} \\ loss=\sum_{u\in\mathcal{U}}\sum_{i\in I_{u}}-\log P_{\theta}(i|u) $$