Ordinal Regression
像分类的回归
考虑一个场景:豆瓣电影评分预测。一共5个档位,从1星到5星。label_set = [1, 2, 3, 4, 5]。很自然的,我们可以把它当作一个经典的多分类问题,模型最后一层通过$softmax$函数输出每一类的概率。然后用$ce\ loss$训练。但是,如果当作分类问题,我们忽略了一点,打分之间是有可比性的:5>4>3>2>1。而如果当作分类问题,经过$one-hot$编码之后,每一个类别是无差别的。
从这个角度看,似乎我们也可以把它当作一个线性回归问题去解决,输出一个连续的打分值,用$mse\ loss$去学习。 那么,到底应该如何选择?
对于这种情况,Ordinal Regression算法似乎更适合些。
Ordinal Regression
说是序数“回归”,它认为本质上是一个考虑了类别间关系的分类算法。如图所示是一个概率函数的分布图。有一个分割点为$c1$,如果我们想求随机变量X小于$c1$的概率$p1=P(X\leq c_1)$,怎么办?
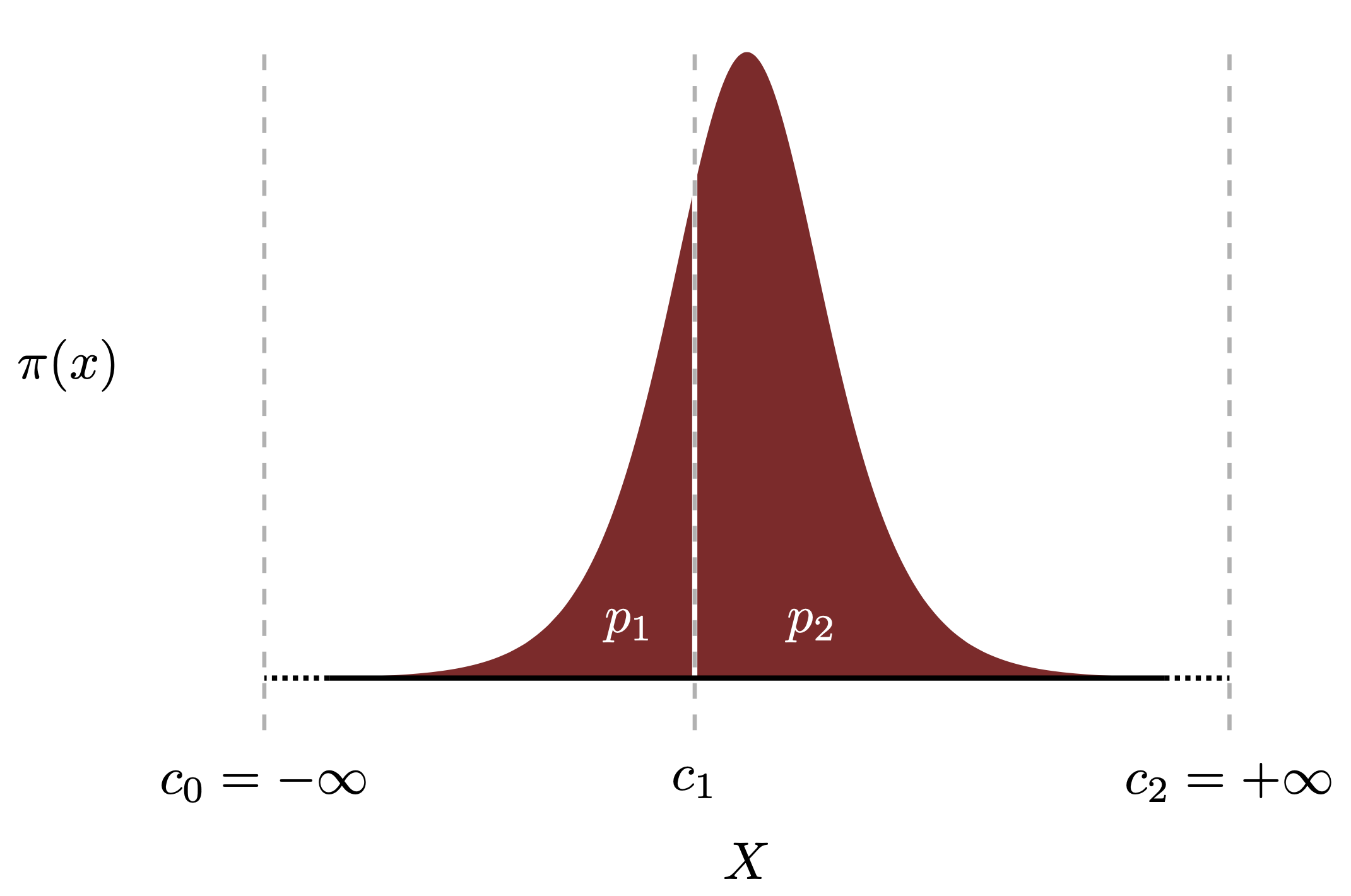
很自然的我们会求该$PDF$的累积分布$CDF$, 有:
$$
p_1=P(X\leq c_1)= \Pi(c_{1}) - \Pi(c_{0}) = \Pi(c_{1}) - 0 = \Pi(c_{1})
$$
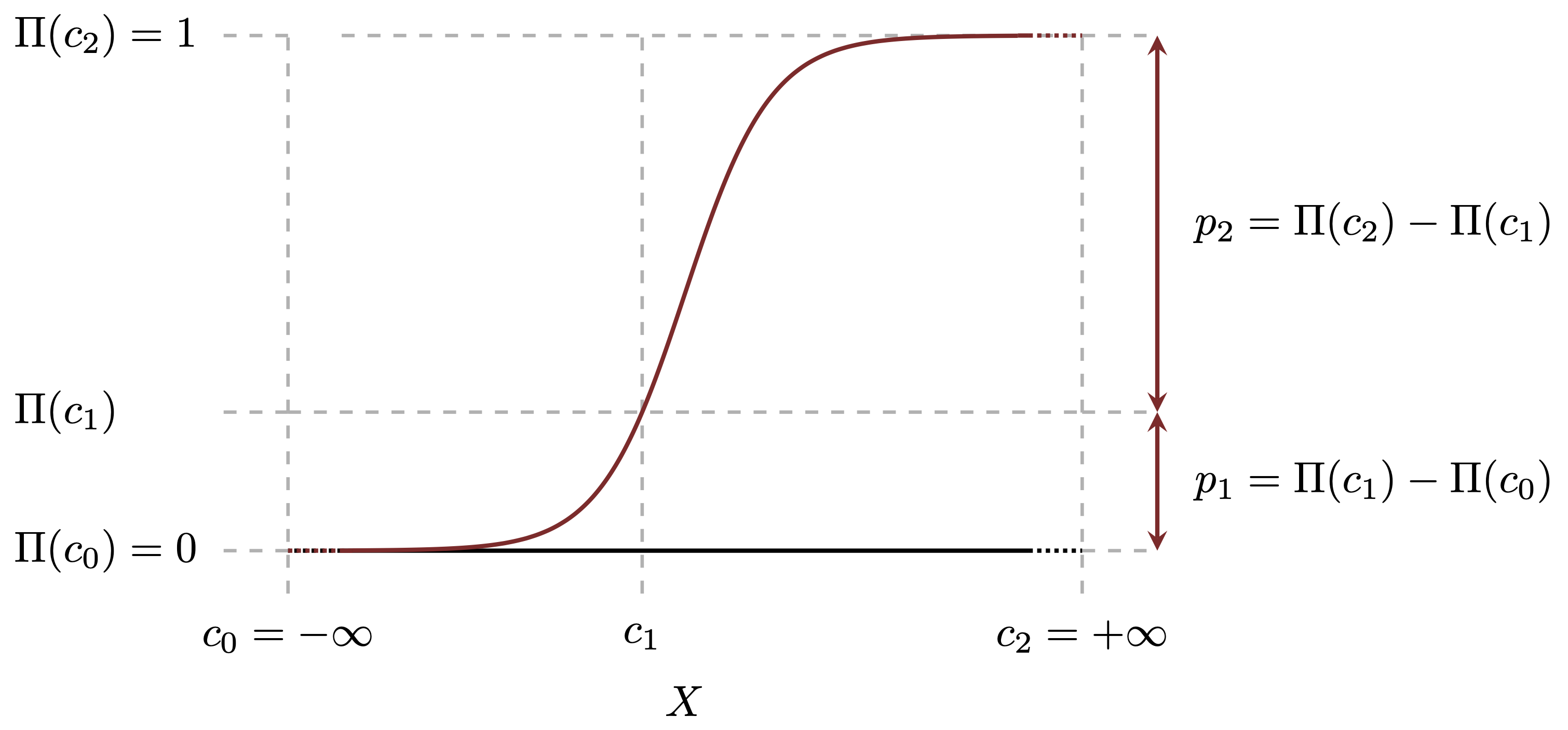
假设我要处理一个5档的分类问题,而上面说的随机变量就是模型的输出,那么问题可以转化为找 到四个切分点$\theta_1,\theta_2,\theta_3,\theta_4$, 并用$P(f(x)<\theta_1),P(\theta_1<f(x)<\theta_2),P(\theta_2<f(x)<\theta_3)$, $P(\theta_3<f(x)<\theta_4),P(\theta_4<f(x)<+\infty)$这五个概率来表示$f(x)$分别属于五个等级的概率。 进一步结合上面的CDF的方法,可以把五个概率转化为: $\Pi(\theta_1-f(x))$, $\Pi(\theta_2-f(x))-\Pi(\theta_1-f(x)), \Pi(\theta_3-f(x))-\Pi(\theta_2-f(x)), \Pi(\theta_4-f(x))-\Pi(\theta_3-f(x)), 1-\Pi(\theta_4-f(x))$
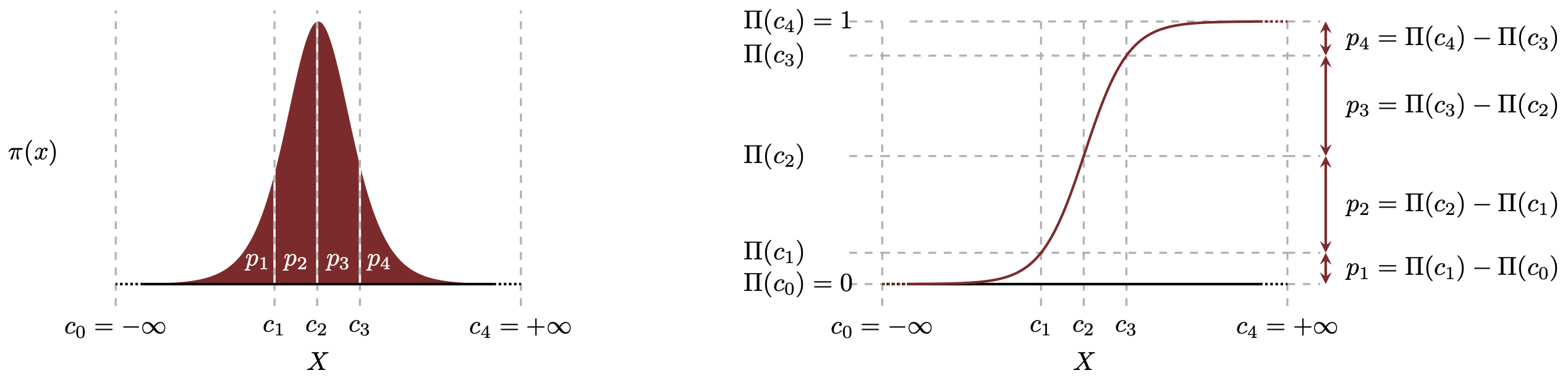
那么,问题来了,$f(x)$该如何表示呢?如何将它与线性模型联系起来呢?让我们先回忆一下线性回归的表达式:
$$ y^*=\mathbf{w}\cdot\mathbf{x}+\varepsilon $$
我们根据$y^{*}$的值所处的区间来预测$y$的类别。如下:
$$ \begin{equation} y=\begin{cases}1 & \mathrm{if~}y^{*}\leq\theta_{1}, \\ 2 & \mathrm{if~}\theta_{1} < y^{*} \leq \theta_{2}, \\ 3 & \mathrm{if~}\theta_{2} < y^{*} \leq \theta_{3}, \\ \vdots \\ K & \mathrm{if~}\theta_{K-1}<y^{*}. \end{cases} \end{equation} $$ 备注: 定义 $\theta_0=-\infty\mathrm{~and~}\theta_K=\infty,y=k\text{ 当且仅当 }\theta_{k-1}<y^*\leq\theta_k.$
写成概率表达,如下:
$$\begin{aligned} P(y=k\mid\mathbf{x})& =P(\theta_{k-1}<y^{*}\leq\theta_k\mid\mathbf{x}) \\ &=P(\theta_{k-1}<\mathbf{w}\cdot\mathbf{x}+\varepsilon\leq\theta_k) \\ &=P(\theta_{k-1} - \mathbf{w}\cdot\mathbf{x} < \varepsilon \leq \theta_k - \mathbf{w}\cdot\mathbf{x}) % &=\Phi(\theta_k-\mathbf{w}\cdot\mathbf{x})-\Phi(\theta_{k-1}-\mathbf{w}\cdot\mathbf{x}) \end{aligned} $$
那么,如果已知$\varepsilon$的PDF,我们就可以从$\varepsilon$的CDF公式进行以上概率的计算。
一般的,我们认为$\varepsilon$服从$logistic$分布,那么$\varepsilon$的CDF便是我们熟悉的$sigmoid$公式: $$\begin{aligned} P(y=k\mid\mathbf{x}) &=P(\theta_{k-1} - \mathbf{w}\cdot\mathbf{x} < \varepsilon \leq \theta_k - \mathbf{w}\cdot\mathbf{x}) \\ &= \sigma(\theta_{k-1} - \mathbf{w}\cdot\mathbf{x}) - \sigma(\theta_{k} - \mathbf{w}\cdot\mathbf{x}) \end{aligned} $$
参考代码:
1#!/usr/bin/env python
2#coding=utf-8
3
4# @Author : whiteding
5# @FileName : ordinal_regression_demo.py
6# @Reference : https://github.com/EthanRosenthal/spacecutter
7
8
9import torch
10import torch.nn as nn
11import torch.optim as optim
12
13class OrdinalRegressionModel(nn.Module):
14 def __init__(self, input_dim, num_classes, scale=20.0):
15 super(OrdinalRegressionModel, self).__init__()
16 self.fc1 = nn.Linear(input_dim, 64)
17 self.fc2 = nn.Linear(64, 32)
18 self.fc3 = nn.Linear(32, 1) # 不管多少类, 输出1个scalar, 类似线性回归
19
20 self.num_classes = num_classes
21 num_cutpoints = self.num_classes - 1
22 # 初始化num_cutpoints个分割点
23 self.cutpoints = torch.arange(num_cutpoints).float()* scale / (num_classes-2) - scale / 2
24 self.cutpoints = nn.Parameter(self.cutpoints)
25
26 def forward(self, x):
27 x = torch.relu(self.fc1(x))
28 x = torch.relu(self.fc2(x))
29 x = self.fc3(x)
30 # [batch_size, num_classes-1]
31 y_pred = self.cutpoints - x
32 return y_pred
33
34# 损失函数
35def cumulative_logit_loss(y_true, y_pred):
36 num_classes = y_pred.size(1) + 1
37 y_true = y_true.long()
38
39 # 注意, 不是softmax, 是sigmoid
40 cumulative_probs = torch.sigmoid(y_pred)
41
42 # [batch_size, num_classes]
43 cumulative_probs = torch.cat([torch.zeros_like(cumulative_probs[:, :1]),
44 cumulative_probs,
45 torch.ones_like(cumulative_probs[:, :1])], dim=1)
46
47 probs = cumulative_probs[:, 1:] - cumulative_probs[:, :-1]
48
49 y_true_one_hot = torch.eye(num_classes)[y_true].to(y_pred.device)
50 log_probs = torch.log(probs + 1e-10)
51
52 loss = -torch.sum(y_true_one_hot * log_probs, dim=1)
53 return loss.mean()
54
55# 创建模型
56input_dim = 10 # 假设输入特征维度为10
57num_classes = 5 # 五个评分等级[0,1,2,3,4]
58model = OrdinalRegressionModel(input_dim, num_classes)
59
60# 训练模型
61optimizer = optim.Adam(model.parameters(), lr=0.001)
62criterion = cumulative_logit_loss
63
64# 生成训练数据
65X_train = torch.rand(100, input_dim)
66y_train = torch.randint(0, num_classes, (100,))
67
68# 训练循环
69for epoch in range(10):
70 model.train()
71 optimizer.zero_grad()
72
73 outputs = model(X_train)
74 loss = criterion(y_train, outputs)
75
76 loss.backward()
77 optimizer.step()
78
79 print(f'Epoch [{epoch+1}/10], Loss: {loss.item():.4f}')