XGBoost的原理分析以及实践
XGBoost算法
原理
任何机器学习的问题都可以从目标函数(objective function)出发，目标函数的主要由两部分组成 $损失函数+正则项$： $$ Obj(\Theta)=L(\Theta)+\Omega(\Theta) $$ 在这里，当选择树模型为基学习器时，需要正则的对象，或者说需要控制复杂度的对象就是这K颗树,通常树的参数有树的深度，叶子节点的个数，叶子节点值的取值(xgboost里称为权重weight)。
所以，我们的目标函数形式如下： $$ \mathcal{L}=\sum_{i} l\left(\hat{y_i}, y_{i}\right)+\sum_{k} \Omega\left(f_{k}\right) $$ 这里前一半代表预测值与真实$label$之间的误差，$i$代表的是每一个训练样本。后一半是正则项，$f_k$代表训练生成的每一颗树。
对一个目标函数，我们最理想的方法就选择一个优化方法算法去一步步的迭代的学习出参数。但是这里的参数是一颗颗的树，没有办法通过这种方式来学习。既然如此，我们可以利用Boosting的思想来解决这个问题，我们把学习的过程分解成先学第一颗树，然后基于第一棵树学习第二颗树。也就是说： $$ \begin{array}{l} \hat{y_i}^{1} = \hat{y_i}^{0}+f_{1}\left(x_{i}\right) \\ \hat{y_i}^{2} = \hat{y_i}^{1}+f_{2}\left(x_{i}\right) \\ ··· \\ \hat{y_i}^{K} = \hat{y_i}^{K-1}+f_{K}\left(x_{i}\right) \\ \end{array} $$
所以，对于第K次的目标函数为： $$ \mathcal{L}^{(K)}=\sum_{i} l\left(y_{i}, \hat{y_i}^{K}\right)+\Omega\left(f_{K}\right)+\text {constant} \\ \mathcal{L}^{(K)}=\sum_{i=1}^{n} l\left(y_{i}, \hat{y_i}^{(K-1)}+f_{K}\left(\mathbf{x_i}\right)\right)+\Omega\left(f_{K}\right) $$ 根据二阶泰勒展开式： $$ f(x+\Delta x)=f(x)+f^{\prime}(x) \Delta x+\frac{1}{2} f^{\prime \prime}(x) \Delta x^{2} $$
令： $$ f(x) = L(y_i, \hat{y_i}^{K-1}) \\ \Delta x = f_K(x_i) $$ 对损失函数二阶展开： $$ \begin{align} \mathcal{L}^{(K)} \simeq \sum_{i} L\left(y_{i}, \hat{y_i}^{K-1}+f_{K}\left(x_{i}\right)\right)=\sum_{i}\left[L\left(y_{i}, \hat{y_i}^{K-1}\right)+L^{\prime}\left(y_{i}, \hat{y_i}^{K-1}\right) f_{K}\left(x_{i}\right)+\frac{1}{2} L^{\prime \prime}\left(y_{i}, \hat{y_i}^{K-1}\right) f_{K}^{2}\left(x_{i}\right)\right] \end{align} $$ 令： $$ \begin{array}{l} g_{i}=L^{\prime}\left(y_{i}, \hat{y_i}^{K-1}\right) \ h_{i}=L^{\prime \prime}\left(y_{i}, \hat{y_i}^{K-1}\right) \end{array} $$ 则进一步得到损失函数为： $$ \mathcal{L}^{(K)} = \sum_{i}\left[L\left(y_{i}, \hat{y_i}^{K-1}\right)+g_{i} f_{K}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{K}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{K}\right)+\text { constant } $$ 一棵树其实可以由一片区域以及若干个叶子节点来表达。而同时，构建一颗树也是为了找到每个节点的区域以及叶子节点的值
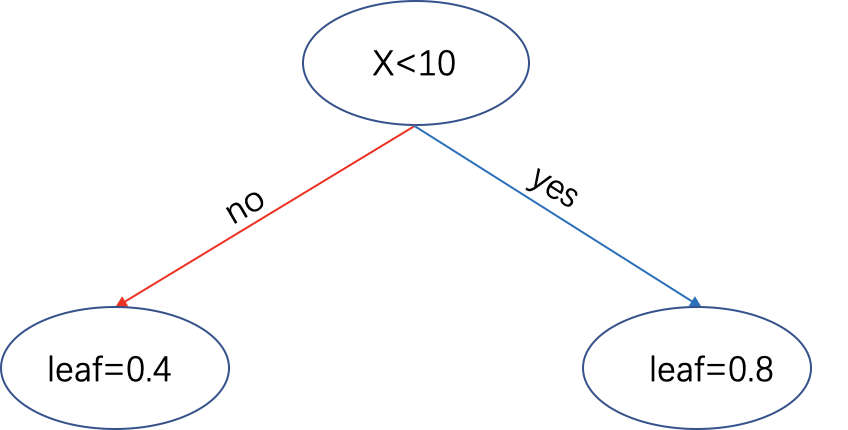$$
f(x)=\begin{cases}0.8&x<10 \\ 0.4&x>=10&\end{cases}
$$
就说可以有如下映射的关系$f_K(x)=w_{q(x)}$。其中$q(x)$为叶子节点的编号（从左往右编，1，2，3···)。$w$是叶子节点的取值。也就说对于任意一个样本$x$,其最后会落在树的某个叶子节点上，其值为$w_{q(x)}$
既然一棵树可以用叶子节点来表达，上面的正则项，我们可以对叶子节点值进行惩罚(正则)，比如取L2正则，以及我们控制一下叶子节点的个数T，那么正则项有： $$ \Omega\left(f_{K}\right)=\frac{1}{2} \lambda \sum_{j}^{T}\left|w_{j}\right|_{2}+\gamma T $$
其实正则为什么可以控制模型复杂度呢？有很多角度可以看这个问题，最直观就是，我们为了使得目标函数最小，自然正则项也要小，正则项要小，叶子节点个数T要小（叶子节点个数少，树就简单）。
而为什么要对叶子节点的值进行L2正则，这个可以参考一下LR里面进行正则的原因，简单的说就是LR没有加正则，整个w的参数空间是无限大的，只有加了正则之后，才会把w的解规范在一个范围内。（对此困惑的话可以跑一个不带正则的LR，每次出来的权重w都不一样，但是loss都是一样的，加了L2正则后，每次得到的w都是一样的）
目标函数（移除常数项后）就可以改写成这样（用叶子节点表达）：
$$ \begin{gathered} \sum_i \left[g_{i}w_{q(x_i)} + \frac{1}{2}h_{i}w_{q(x_i)}^2 \right] + \frac{1}{2}\lambda\sum_j^T\left|w_j\right|_2 + \gamma T \\ =\sum_{j=1}^{T} \left[\left(\sum_{i\in {I_j}}g_i \right)w_j+\frac{1}{2}\left(\sum_{i \in {I_j}}h_i+\lambda\right)w_{j}^2\right]+\gamma(T) \end{gathered} $$ 令：
$$ \begin{aligned} G_{j} &=\sum_{\left(i \in I_{j}\right)} g_{i} \\ H_{j} &=\sum_{\left(i \in I_{j}\right)} h_{i} \end{aligned} $$
$$ \sum_{j=1}^{T}\left[G_{j} w_{j}+\frac{1}{2}\left(H_{j}+\lambda\right) w_{j}^{2}\right]+\gamma T $$
对$w_j$求导，然后带入极值点，可以得到一个极值 $$ w^{*}=-\frac{G_{j}}{H_{j}+\lambda} \\ \mathcal{L} = -\frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}^{2}}{H_{j}+\lambda}+\gamma T $$ 到这里，我们一直都是在围绕目标函数进行分析，这个到底是为什么呢？这个主要是为了后面我们寻找$f(x)$，也就是建树的过程。
具体来说，我们回忆一下建树的时候需要做什么，建树的时候最关键的一步就是选择一个分裂的准则，也就如何评价分裂的质量。比如在GBDT的介绍里，我们可以选择MSE，MAE来评价我们的分裂的质量，但是，我们所选择的分裂准则似乎不总是和我们的损失函数有关，因为这种选择是启发式的。比如，在分类任务里面，损失函数可以选择logloss，分裂准确选择MSE，这样看来，似乎分裂的好坏和我们的损失并没有直接挂钩。
但是，在xgboost里面，我们的分裂准则是直接与损失函数挂钩的准则，这个也是xgboost和GBDT一个很不一样的地方。
具体来说，$XGBoost$选择这个准则，计算增益$Gain$ $$ {Gain}=\frac{1}{2}\left[\frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{G_{R}^{2}}{H_{R}+\lambda}-\frac{\left(G_L+G_{R}\right)^{2}}{\left(H_{L}+H_{R}\right)+\lambda}\right]-\gamma $$ 为什么?其实选择这个作为准则的原因很简单也很直观。 我们这样考虑。由损失函数的最终表达式知道，对于一个结点，假设不分裂的话, 此时该节点损失为: $$ -\frac{\left(G_L+G_{R}\right)^{2}}{\left(H_{L}+H_{R}\right)+\lambda} $$ 分裂之后左右子节点总损失为： $$ -\left[\frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{G_{R}^{2}}{H_{R}+\lambda}\right] $$ 既然要分裂的时候，我们当然是选择分裂成左右子节点后，损失减少的最多, 即找到分裂点，使得: $$ \max \left(\left[\frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{G_{R}^{2}}{H_{R}+\lambda}-\frac{\left(G_L+G_{R}\right)^{2}}{\left(H_{L}+H_{R}\right)+\lambda}\right]\right) $$ 那么$\gamma$的作用是什么呢？利用$\gamma$可以控制树的复杂度，进一步来说，利用$\gamma$来作为阈值，只有大于$\gamma$时候才选择分裂。这个其实起到预剪枝的作用。
寻找分裂点算法
缺失值的处理
从上图中可以看到,内层循环里面有两个for，第一个for是从把特征取值从小到大排序，然后从小到大进行扫描，这个时候在计算$G_R$的时候是用总的$G$减去$G_LG_R$时候是用总的$G$减去$G_L$，$H_R$也是同样用总的$H$减去$H_L$,这意味着把空缺样本归到了右子结点。
第二个for相反过来，把空缺样本归到了左子结点。 只要比较这两次最大增益出现在第一个for中还是第二个for中就可以知道对于空缺值的分裂方向，这就是xgboost如何学习空缺值的思想。
特征重要性
一般我们调用xgb库的get_fscore()。但其实xgboost里面有三个指标用于对特征进行评价，而get_fscore()只是其中一个指标weight。这个指标大部分玩家都很熟悉，其代表着某个特征被选作分裂的次数。
而xgboost还提供了另外两个指标，一个叫gain，一个叫cover。可以利用get_score()来选择。
那么gain是指什么呢？其代表着某个特征的平均增益。 比如，特征x1被选了6次作为分裂的特征，每次的增益假如为Gain1,Gain2,…Gain6，那么其平均增益为$(Gain1+Gain2+…Gain3)/6$
实践
| ID | x1 | x2 | y |
|---|---|---|---|
| 1 | 1 | -5 | 0 |
| 2 | 2 | 5 | 0 |
| 3 | 3 | -2 | 1 |
| 4 | 1 | 2 | 1 |
| 5 | 2 | 0 | 1 |
| 6 | 6 | -5 | 1 |
| 7 | 7 | 5 | 1 |
| 8 | 6 | -2 | 0 |
| 9 | 7 | 2 | 0 |
| 10 | 6 | 0 | 1 |
| 11 | 8 | -5 | 1 |
| 12 | 9 | 5 | 1 |
| 13 | 10 | -2 | 0 |
| 14 | 8 | 2 | 0 |
| 15 | 9 | 0 | 1 |
导数公式
由于后面需要用到logloss的一阶导数以及二阶导数，这里先简单推导一下： $$ L_{i}=-\left[y_{i} \cdot \textit{log} \left(p_{i}\right)+\left(1-y_{i}\right) \cdot \textit{log} \left(1-p_{i}\right)\right] $$ 其中： $$ p_i=\sigma(\hat y_i)=\frac{1}{1+e^{\hat {-y_i}}} $$
$$ \begin{aligned} \frac{\partial L_{i}}{\partial\hat {y_i}} &= \frac{\partial L_{i}}{\partial p_{i}} \cdot \frac{\partial p_{i}}{\partial \hat {y_i}} \\ &=\sigma\left(\hat {y_i}\right)-y_{i} \end{aligned} $$
即： $$ g_i = \sigma\left(\hat {y_i}\right)-y_{i} $$ 同理二阶导数： $$ h_{i}=\sigma (\hat {y_i}) *\left(1-\sigma (\hat {y_i})\right) $$
建立第一颗树(k=1)
根据公式： $$ \max \left(\left[\frac{G_{L}^{2}}{H_{L}+\lambda}+\frac{G_{R}^{2}}{H_{R}+\lambda}-\frac{\left(G_L+G_{R}\right)^{2}}{\left(H_{L}+H_{R}\right)+\lambda}\right]\right) $$ 在结点处把样本分成左子结点和右子结点两个集合。分别求两个集合的$H_L,H_R, G_L, G_R$，然后计算增益$Gain$
但是这里你可能碰到了一个问题，那就是第一颗树的时候每个样本的预测的概率值$\sigma (\hat {y_i})$是多少？
这里和GBDT一样，应该说和所有的Boosting算法一样，都需要一个初始值。而在xgboost里面，对于分类任务只需要初始化为(0,1)中的任意一个数都可以。具体来说就是参数base_score。（其默认值是0.5)
这里我们也设base_score=0.5(即$\hat{y_i}^{0}= 0$)。然后我们就可以计算每个样本的一阶导数值和二阶导数值了
$$ \begin{array}{|l|l|l|l|l|l|l|l|l|l|l|l|l|l|l|l|} \hline{ID} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 \\ \hline{g_i} & 0.5 & 0.5 & -0.5 & -0.5 & -0.5 & -0.5 & -0.5 & 0.5 & 0.5 & -0.5 & -0.5 & -0.5 & 0.5 & 0.5 & -0.5 \\ \hline{h_i} & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 & 0.25 \\ \hline \end{array} $$
那么把样本如何分成两个集合呢？这里就是上面说到的选取一个最佳的特征以及分裂点使得GainGain最大。
比如说对于特征$x_1$，一共有[1, 2, 3, 6, 7, 8, 9, 10]8种取值。可以得到以下这么多划分方式: $$ x_1 < 2 \ \ \ x_1<3 \ \ \ x_1<4 ··· $$ 分别计算不同的分割点得到： $$ \begin{array}{|l|l|l|l|l|l|l|l|} \hline{split_point} & 2 & 3 & 6 & 7 & 8 & 9 & 10 \\ \hline{G_L} & 0 & 0 & -0.5 & -1 & -1 & -1 & -2 \\ \hline{H_L} & 0.5 & 1 & 1.25 & 2 & 2.5 & 3 & 3.5 \\ \hline{G_R} & -1.5 & -1.5 & -1 & -0.5 & -0.5 & -0.5 & 0.5 \\ \hline{H_R} & 3.25 & 2.75 & 2.5 & 1.75 & 1.25 & 0.75 & 0.25 \\ \hline{Gain} & 0.0557275 & 0.1263157 & -0.0768588 & -0.0494417 & -0.0768588 & -0.0808270 & 0.6152046 \\ \hline \end{array} $$ 从上表我们可以到，如果特征$x_1$以$x_1<10$分裂时可以得到最大的增益$0.615205$
同理，遍历下一个特征$x_2$，可以得到类似的表如下: $$ \begin{array}{|l|l|l|l|l|} \hline{split_point} & -2 & 0 & 2 & 5 \\ \hline{G_L} & -0.5 & 0 & -1.5 & -1 \\ \hline{H_L} & 0.75 & 1.5 & 2.25 & 3 \\ \hline{G_R} & -1 & -1.5 & 0 & -0.5 \\ \hline{H_R} & 3 & 2.25 & 1.5 & 0.75 \\ \hline{Gain} & -0.080827067669 & 0.218623481781 & 0.218623481781 & -0.080827067669 \\ \hline \end{array} $$ 可以看到，以$x_2$特征来分裂时，最大的增益是$0.2186<0.615205$。所以在根节点处，我们以$x_1<10$来进行分裂。
由于设置的最大深度是3，此时只有1层，所以还需要继续往下分裂。分裂过程如上所述，不再赘述。
最终我们得到了训练好的第一个树：
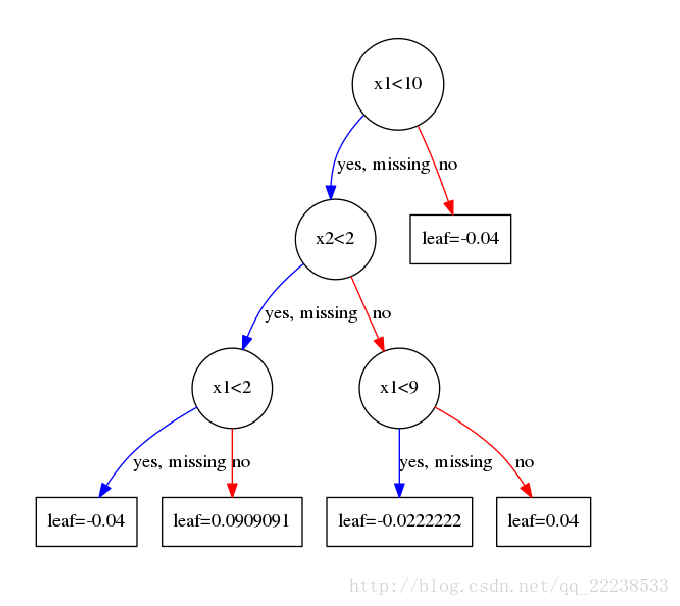
注意：
这里可能对叶子结点取值感到困惑。为何算出来的是-0.4，可图上却是-0.04？
比如第一次分裂的右节点，根据公式 $$ w^{*}=-\frac{G_{j}}{H_{j}+\lambda} = -\frac{0.5}{0.25+1} = -0.4 \ \ \ \ \ (\lambda=1) $$ 这里其实和我们在GBDT中的处理一样，我们会以一个学习率来乘这个值，当完全取-0.4时说明学习率取1，这个时候很容易过拟合。所以每次得到叶子结点的值后需要乘上学习率$\eta$，在前面我们已经设置了学习率是0.1。这里也是GBDT和xgboost一个共同点，大家都是通过学习率来进行Shrinkage，以减少过拟合的风险。
至此，我们学习完了第一颗树。
建立第2颗树(k=2)
我们开始拟合我们第二颗树。其实过程和第一颗树完全一样。只不过对于$\sigma (\hat {y_i})$需要进行更新，也就是拟合第二颗树是在第一颗树预测的结果基础上。这和GBDT一样，因为大家都是Boosting思想的算法。
在第一颗树里面由于前面没有树，所以初始$\sigma (\hat {y_i}) = 0.5$（相当于第0棵树）
假设此时，模型只有这一颗树(K=1)，那么模型对样例$x_i$进行预测时，预测的结果表达是什么呢？
根据我们之前原理部分的推导: $$ \begin{array}{l} y_{i}^{K}=\sum_{k=0}^{K} f_{k}\left(x_{i}\right) \\ y_{i}^{1}=f_{0}\left(x_{i}\right)+f_{1}\left(x_{i}\right) \end{array} $$ $f_1(x_i)$的值是样例$x_i$落在第一棵树上的叶子结点值。则经过第0、1颗树的预测值为： $$ \hat{y_i}^{1}=f_{0}\left(x_{i}\right)+f_{1}\left(x_{i}\right) = 0 + w_{q(x_i)} $$ 我们可以得到第一棵树预测为正样本的概率为下表：
| ID | $\sigma(\hat{y_i}^{1})$ |
|---|---|
| 1 | 0.490001 |
| 2 | 0.494445 |
| 3 | 0.522712 |
| 4 | 0.494445 |
| 5 | 0.522712 |
| 6 | 0.522712 |
| 7 | 0.494445 |
| 8 | 0.522712 |
| ··· | ··· |
比如对于ID=1的样本，其落在$-0.04$这个节点。那么经过$sigmod$映射后的值： $$ p_{1}=\frac{1}{1+e^{-(0-0.04)}}=0.490001 $$ 有了这个之后，我们就可以计算所有样本新的一阶导数和二阶导数的值了。具体如下表：
| ID | $g_i$ | $h_i$ |
|---|---|---|
| 1 | 0.490001320839 | 0.249900026415 |
| 2 | 0.490001320839 | 0.24996913829 |
| 3 | -0.477288365364 | 0.249484181652 |
| 4 | -0.505555331707 | 0.24996913829 |
| 5 | -0.477288365364 | 0.249484181652 |
| ··· | ··· | ··· |
拟合完后第二颗树如下图:
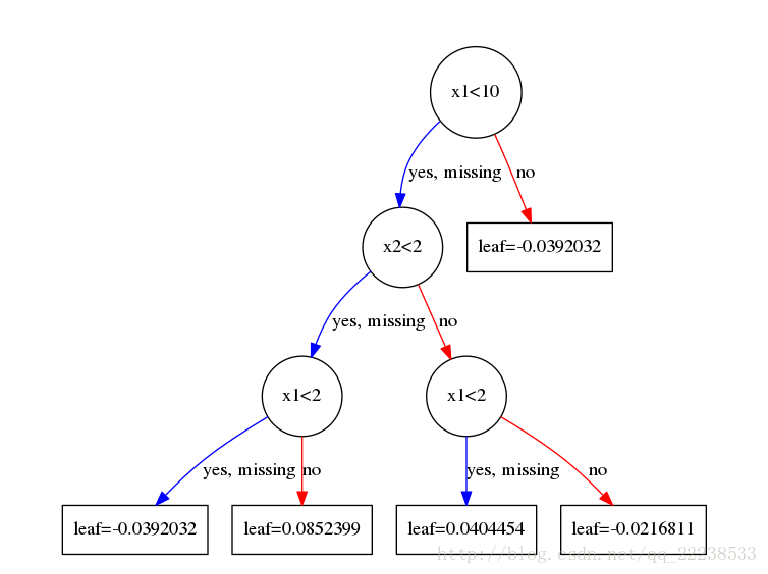
后面的所有过程都是重复这个过程，这里就不再啰嗦了。
其他细节
参数: $min\_child\_weight$
根据官网的解释，$sum\ of\ instance\ weight(hessian)$也就是对应这个： $$ H_{j}=\sum_{i \in I_{j}} h_{i} $$ 也就是说，在进行分裂时，分裂后的每个节点上所有样本对应的$h_i$之和不应该小于这个参数
举例来说，在我们训练第一个树时，第一次分裂，我们选择$x_1<10$.分裂后的右节点只有一个样本，此时$\sum{H_R} = 0.25$, 如果我们设置$min\_child\_weight = 0.26$，那么就不应该以$x_1<10$分裂，而是退一步考虑次最大增益。
参数$\gamma$
前面训练过程中，我们把$\gamma$设成了0，如果我们设置成其他值比如1的话，在考虑最大增益的同时，也要考虑这个最大的增益是否比$\gamma$大，如果小于$\gamma$则不进行分裂（预剪枝）
缺失值的处理
xgboost对缺失值的处理思想很简单，具体看下面的算法流程：
简单来说，就是把缺失值对应的样本分别全部放到左、右节点里，看哪一种情况对应的 $Gain$值最大。
xgboost如何用于特征选择:
