模型特征重要性的计算
深度学习的兴起,使得各种复杂的NN网络应用变得流行。但是,对于这些黑盒的模型,我们一般很难知晓哪些特征对模型的学习比较重要, 即对缺乏特征重要性的解释。这里,我们会介绍一些主流的方法,来计算模型特征的重要性。
Tree_base
树模型的解释性一般要优于NN模型,因为书模型的学习是可解释的,大多数Tree模型也都带有查看特征重要性的接口,以xgboost为例:
xgboost如何用于特征选择:

缺点: 无法迁移到NN模型上。
NN model
单特征 auc
- 特征值置为 0
- 特征取随机值
- 特征值随机打乱
看单特征的重要性,通过随机扰乱等方法一般比较直观,但是运算量巨大。
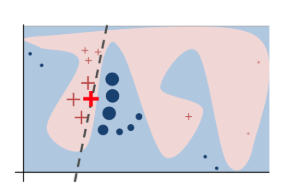
LIME
- 选择一个数据点:选择需要解释的单个数据点。
- 生成邻域数据:在该点周围生成一组类似的样本数据,并使用原始模型进行预测。
- 权重计算:根据与原始数据点的相似度,为这些新样本赋予权重。
- 拟合局部线性模型:使用加权线性回归模型在局部数据上进行训练。
- 解释模型:通过局部线性模型的系数来解释特定数据点的预测结果。
1import numpy as np
2import sklearn
3from sklearn.linear_model import LinearRegression
4from sklearn.metrics.pairwise import euclidean_distances
5
6# 假设你有一个训练好的DNN模型
7def predict_fn(X):
8 # 替换为实际的模型预测函数
9 return model.predict(X)
10
11# 生成邻域数据
12def generate_neighborhood_data(instance, num_samples=5000, scale=0.1):
13 neighborhood_data = np.random.normal(loc=instance, scale=scale, size=(num_samples, instance.shape[0]))
14 return neighborhood_data
15
16# 计算权重
17def calculate_weights(instance, neighborhood_data, kernel_width=0.75):
18 distances = euclidean_distances(neighborhood_data, instance.reshape(1, -1)).ravel()
19 weights = np.exp(-distances**2 / (2 * kernel_width**2))
20 return weights
21
22# 解释函数
23def lime_explanation(instance, predict_fn, num_samples=5000):
24 # 生成邻域数据
25 neighborhood_data = generate_neighborhood_data(instance, num_samples)
26
27 # 获取邻域数据的预测结果
28 predictions = predict_fn(neighborhood_data)
29
30 # 计算权重
31 weights = calculate_weights(instance, neighborhood_data)
32
33 # 拟合局部线性模型
34 model = LinearRegression()
35 model.fit(neighborhood_data, predictions, sample_weight=weights)
36
37 # 返回线性模型的系数作为特征重要度
38 return model.coef_
39
40# 示例使用
41instance = np.array([0.5, 0.3, 0.2, 0.1, 0.4]) # 需要解释的实例
42feature_importances = lime_explanation(instance, predict_fn)
43print("Feature importances:", feature_importances)
SHAP分析
SHAP 算法的原理步骤如下:
- 特征组合:考虑所有可能的特征子集。
- 边际贡献:计算每个特征加入现有特征子集后对模型输出的边际贡献。
- 平均边际贡献:对所有特征子集计算每个特征的平均边际贡献,得到Shapley值。
1举个例子:
2一个DNN模型有5个特征<x_1, x_2, x_3, x_4, x_5>
3x_5的Shapley值为:<x_1, x_2, x_3, x_4>特征集合的所有子集加上x_5所取得的边际增益的平均值
4
5Shapley_value = avg([Model(x1, x5) - Model(x5)], [Model(x1, x2, x5) - Model(x1, x2)], [Model(x1, x2, x3, x5) - Model(x1, x2, x3)],···)
SENet
为每一个特征(field)学习不同的权重。有利于模型的特征进行加权,无效特征进行降权.
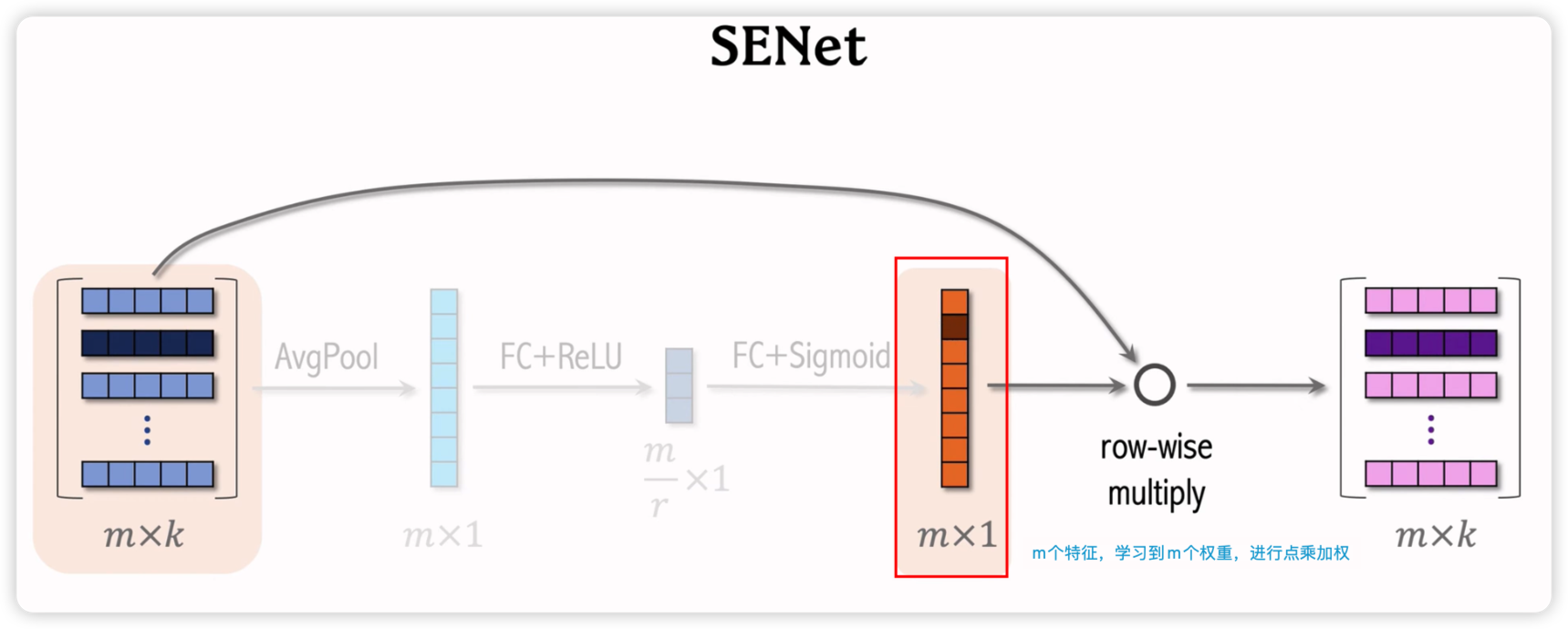

关于计算权重最后的激活函数的说明:
- 用$sigmoid$函数,每个权重限制在$0~1$之间,意味着好的特征不进行打压,维持现状(权重接近于1),不好的特征进行抑制(权重接近于0)
- 用$2*sigmoid$函数, 每个权重限制在$0~2$之间,意味着好的特征进行加权,(权重接>1.0),不好的特征进行抑制(权重接系小于1.0)
- 用$relu$函数,每个权重限制在$0~\infty$之间,意味着好的特征进行加权,(权重接>1.0),不好的特征进行drop(权重等于0)