Transformer的细节
Transformer中的几个细节讨论
1. 为什么self-attention中需要$/\sqrt{d}$
在自注意力(self-attention)机制中,将查询(Query, Q)与键(Key, K)相乘之后除以($\sqrt{d}$),其中d是键向量的维度,这是为了稳定梯度和防止数值不稳定。
具体原因如下:
-
避免数值过大:在没有缩放的情况下,Q和K的点积结果会随着维度$d$的增加而变得很大。点积的结果会随着维度的增加而呈线性增长,使得softmax函数的输入值很大,这会导致梯度消失(vanishing gradients)问题。
-
稳定softmax函数:将点积结果除以$\sqrt{d}$可以将其值缩小到一个相对较小的范围,从而使得softmax函数的输出更加平滑和稳定。softmax的输入值太大时,其梯度会非常小,使得模型训练变得困难。
从数学上来说,假设查询向量和键向量中的每个元素都是独立同分布的零均值单位方差的高斯随机变量,那么它们的点积的期望值是0,方差是$d$。通过除以$\sqrt{d}$,我们可以使得点积的方差变为1,这样可以保持数值的稳定性。
让我们更详细地探讨一下为什么在自注意力机制中对 Q 和 K 的点积进行缩放可以将方差变为 1。
假设查询向量 $Q$ 和键向量 $K$ 的每个元素都是独立同分布的零均值单位方差的高斯随机变量。我们可以对 Q 和 K 的点积进行一些简单的数学分析。
设 $Q$ 和 $K$ 的维度为 $d$,即: $$ Q = [q_1, q_2, \ldots, q_d] \\ K = [k_1, k_2, \ldots, k_d] $$ 其中 $q_i$ 和 $k_i$ 都是独立同分布的随机变量,均值为0,方差为1。我们来看 Q 和 K 的点积 $Q \cdot K$:
$$ Q \cdot K = \sum_{i=1}^d q_i k_i $$
由于 $q_i$ 和 $k_i$ 是独立的随机变量,它们的乘积 $q_i k_i$ 也是随机变量。对于这些随机变量 $q_i k_i$ 的和,我们可以用期望和方差的性质来分析。
期望(Expectation):
$$ E[q_i k_i] = E[q_i] E[k_i] = 0 \times 0 = 0 $$
因此,所有 $q_i k_i$ 的期望都是0,所以:
$$ E\left[\sum_{i=1}^d q_i k_i\right] = \sum_{i=1}^d E[q_i k_i] = \sum_{i=1}^d 0 = 0 $$
方差(Variance):
由于 $q_i$ 和 $k_i$ 是独立的,$q_i k_i$ 的方差为: $$ \text{Var}(q_i k_i) = E[(q_i k_i)^2] - (E[q_i k_i])^2 = E[(q_i k_i)^2] $$
因为 $q_i$ 和 $k_i$ 都是零均值、单位方差的高斯分布随机变量,我们有: $$ E[(q_i k_i)^2] = E[q_i^2] E[k_i^2] = 1 \times 1 = 1 $$ 所以,$q_i k_i$ 的方差是1。
由于 $q_i k_i$ 是独立的随机变量,我们可以直接求和的方差:
$$ \text{Var}\left(\sum_{i=1}^d q_i k_i\right) = \sum_{i=1}^d \text{Var}(q_i k_i) = \sum_{i=1}^d 1 = d $$
因此,点积 $Q \cdot K$ 的方差为 $d$。为了使得点积的方差变为1,我们需要将点积缩放,使其除以 $\sqrt{d}$:
$$ \text{Var}\left(\frac{Q \cdot K}{\sqrt{d}}\right) = \frac{\text{Var}(Q \cdot K)}{d} = \frac{d}{d} = 1 $$
这就是为什么在自注意力机制中,我们将 Q 和 K 的点积除以 $\sqrt{d}$。这样做可以确保缩放后的点积具有方差为1的标准正态分布,从而保持数值稳定性并有助于梯度的有效传递。
2. Transformer为何使用多头注意力机制
Transformer 使用多头注意力机制(Multi-Head Attention)的主要原因是为了增强模型的表示能力和捕捉不同的特征信息。具体来说,多头注意力机制提供了以下几个关键优势:
-
捕捉不同的子空间信息:每个注意力头都可以在不同的子空间中学习并关注不同的特征信息。这样,多个注意力头可以捕捉到输入序列中的不同空间的关系,这比单一的注意力头更为强大,类比CNN的多个卷积核。
-
提升模型的稳定性:通过将多个注意力头的结果进行拼接和线性变换,多头注意力机制可以降低单个注意力头不稳定的影响,从而使得模型更加鲁棒。
-
丰富表示能力:多头注意力机制允许模型在不同的子空间中学习更丰富的表示,这有助于模型更好地理解和生成复杂的序列数据。
多头 VS 单头参数量比较:
- 单头注意力的参数
在单头注意力机制中,查询(Query, Q)、键(Key, K)和值(Value, V)是通过输入 $X$ 线性变换得到的:
$ Q = XW_Q, \quad K = XW_K, \quad V = XW_V $
其中 $W_Q$、$W_K$ 和 $W_V$ 的维度均为 $d_{model} \times d_{model}$,因此单头注意力的参数总量为:
$$ \text{参数量}_\text{单头}=d_{model}\times d_{model}+d_{model}\times d_{model}+d_{model}\times d_{model}=3d_{model}^2 $$
- 多头注意力的参数
在多头注意力机制中,我们将查询、键和值分别投影到多个子空间中。假设每个注意力头的维度为 $d_k$ 和 $d_v$,通常 $d_k = d_v = d_{model} / h$。对于每个头 $i$,查询、键和值的线性变换如下:
$$ Q_i = XW_{Q_i}, \quad K_i = XW_{K_i}, \quad V_i = XW_{V_i} $$
其中 $W_{Q_i}$、$W_{K_i}$ 和 $W_{V_i}$ 的维度均为 $d_{model} \times d_k$。由于有 $h$ 个头,总的参数量为:
$$ \text{参数量}_{\text{投影}} = h \times (d_{model} \times d_k + d_{model} \times d_k + d_{model} \times d_v) = h \times 3 \times d_{model} \times \frac{d_{model}}{h} = 3d_{model}^2 $$
最后,多头注意力机制的输出还需要一个线性变换矩阵 $W_O$ 将拼接后的结果变换回 $d_{model}$ 维度:
线性变换矩阵 $W_O$ 的参数量为:
$$ \text{参数量}_{W_O} = d_{model} \times d_{model} = d_{model}^2 $$
总的参数量:
将所有参数量相加,多头注意力的总参数量为:
$$ \text{参数量}_{\text{多头}} = 3d_{model}^2 + d_{model}^2 = 4d_{model}^2 $$
3. Feed Forward层参数
$Feed\ Forward$网络中的参数通常是对每个位置或每个token是共享的, 具体来说,在Transformer模型中,每个位置的$Feed\ Forward$网络包含两层全连接层。
一般地,第一个线性层是先将维度从$h$ 映射到 $4h$ ,第二个线性层再将维度从4$h$映射到$h$。第一个线性层的权重矩阵$W_1$ 的形状为 $[h,4h]$ ,偏置的形状为 $[4h]$ 。第二个线性层权重矩阵$W_2$的形状为$[4h,h]$ ,偏置形状为$[h]$ 。MLP块的参数量为$8h^2+5h$ 。
4. Decoder的输入
在train模式下和在test模式下Decoder的输入是不同的,在train模式下Decoder的输入是$Ground\ Truth$,也就是不管输出是什么,会将正确答案当做输入,这种模式叫做$teacher-forcing$。
但是在test模式下根本没有$Ground\ Truth$去teach,那只能将已经出现的词的输出(注意这里的输出是softmax预测的结果)当做下一次Decoder计算的输入,这也是论文中$shifted\ right$的意思,一直往右移。
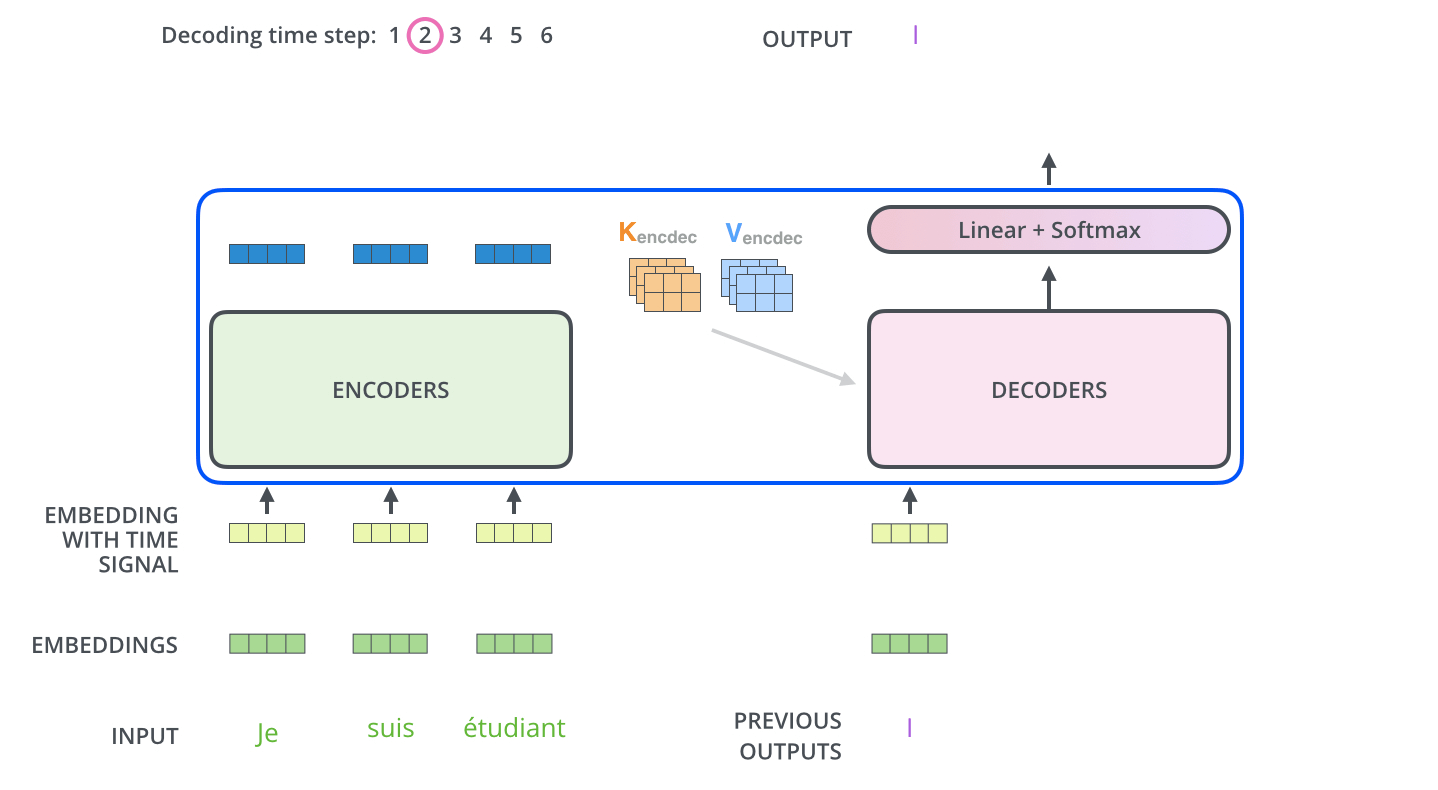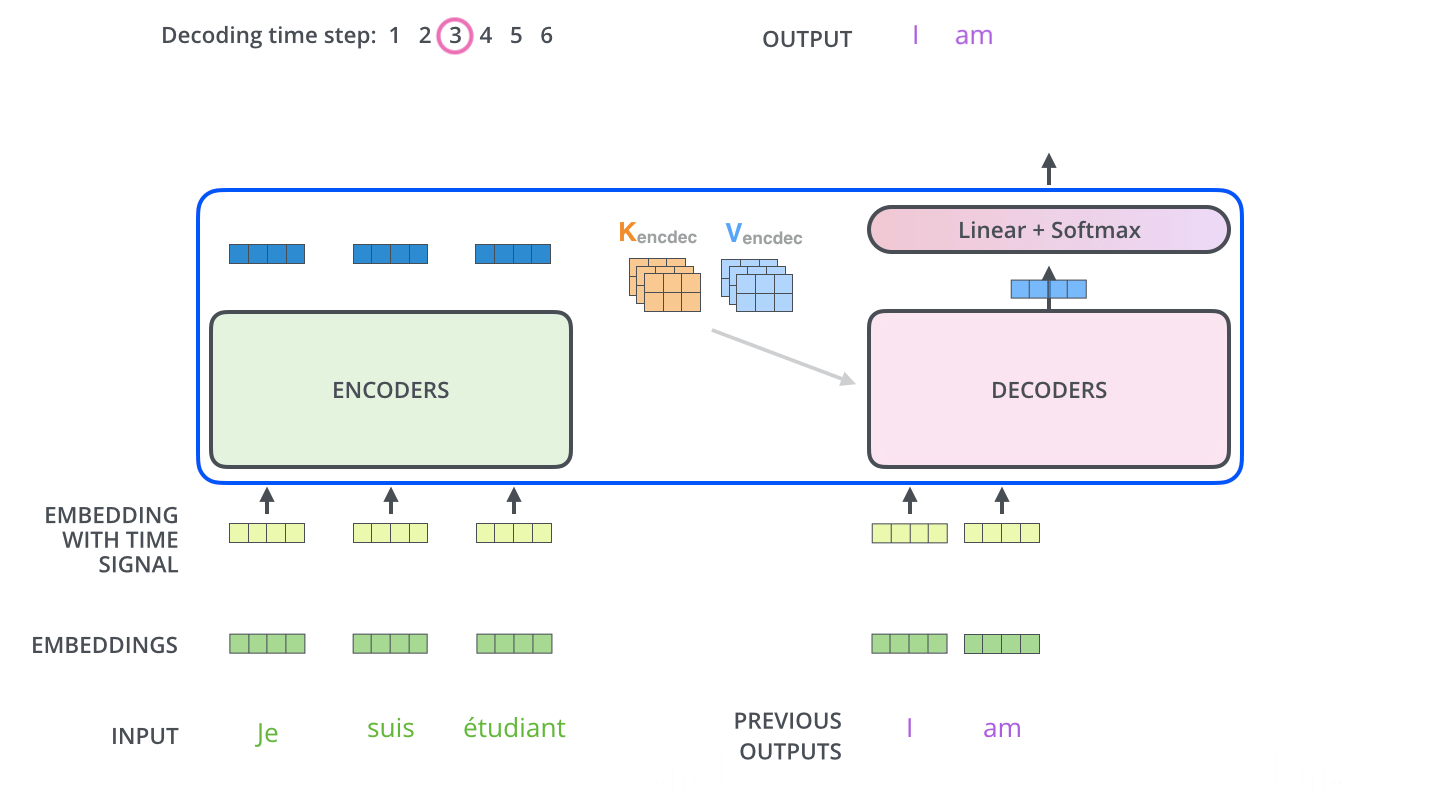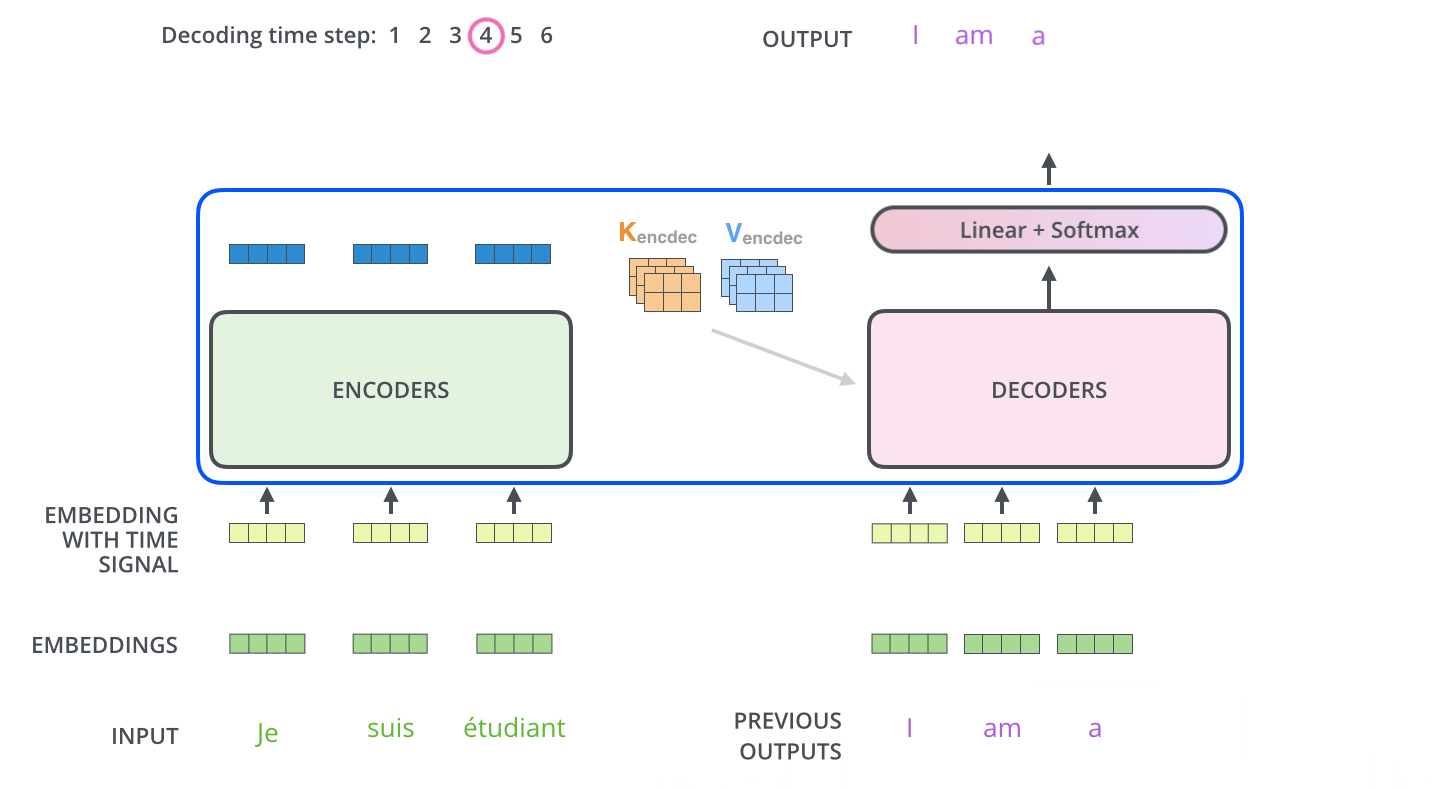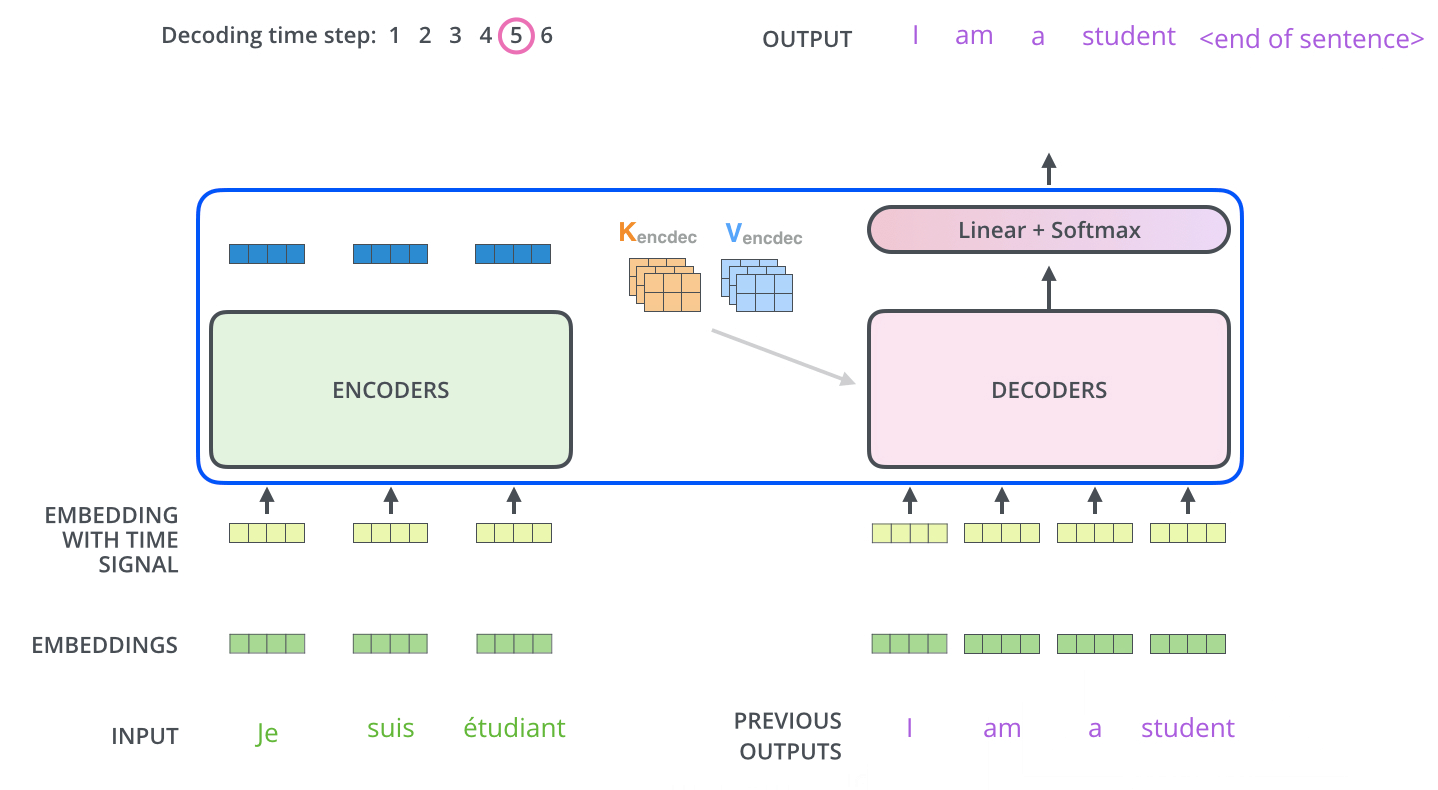
5. Decoder到底是不是并行计算的
在Transformer中,最被人津津乐道,也是他相较于RNN类型模型最大的优点之一就是他可以并行计算,但是这个并行计算仅限于在Encoder中,在Encoder中是将所有的词一起输入一起计算。
但是在Decoder中不是的,在Decoder中依然是像RNN一样一个一个词输入,将已经出现的词计算得到的Q与Encoder计算得到的K,V进行计算,经过了全部Decoder层再经过FC+Softmax得到结果之后再把结果当做Decoder的输入再走一遍整个流程直到得到END标签。
但是,在训练的阶段,由于$teacher-forcing$的机制存在,Encoder也是并行的,因为我们是知道正确答案的。但是,在预测时,必须遵循$next-token$的预测机制,也就是说只能是串行的。
所以:
在训练阶段,是并行的
在预测阶段,是串行的
5.Transformer的参数量估计
