对比损失中温度系数的作用
温度系数
对比损失(Contrastive Loss)中的参数$\tau$是一个神秘的参数,大部分论文都默认采用较小的值来进行自监督对比学习(例如 $\tau = 0.05$),但是很少有文章详细讲解参数$\tau$的作用,本文将详解对比损失中的超参数 ,并借此分析对比学习的核心机制。
首先总结下本文的发现:
-
对比损失是一个具备困难负样本自发现性质的损失函数,这一性质对于学习高质量的自监督表示是至关重要的。关注困难样本的作用是:对于那些已经远离的负样本,不需要让其继续远离,而主要聚焦在如何使没有远离的负样本远离,从而使得表示空间更均匀(Uniformity)
-
$\tau$的作用是调节模型困难样本的关注程度:$\tau$越小,模型越关注于将那些与本样本最相似的负样本分开
带有温度系数的对比损失形式如下:
$$ \mathcal{L}(x_i)=-\log\left[\frac{\exp(s_{i,i}/\tau)}{\sum_{k\neq i}\exp(s_{i,k}/\tau)+\exp(s_{i,i}/\tau)}\right] $$
-
原始的$softmax$的输入形式如下:
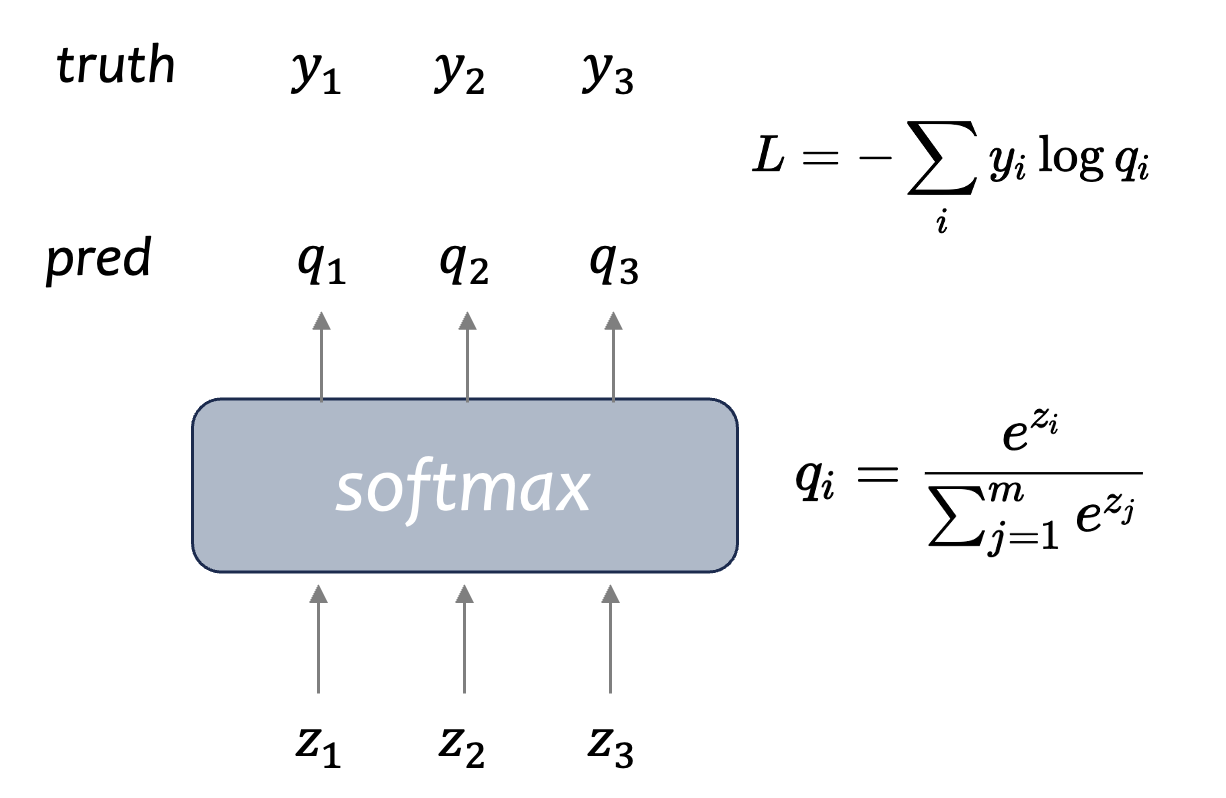
-
加上温度系数之后的影响:
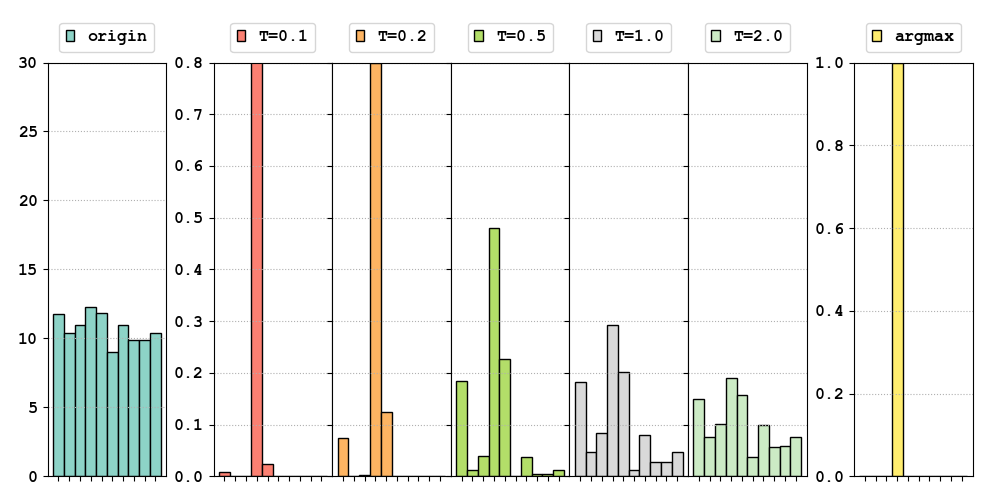
备注:最左边是我们随机生成的分布,来模拟softmax的输入$\mathbf{z}\in\mathbb{R}^{10}\sim N(10,1)$。中间五幅图是使用softmax得到的结果, 纵坐标等价于$q$。其中温度系数 $\tau = 1.0$时相当于原始的softmax。右侧对比了$argmax$得到的结果。
可以看到,在输入差距不大的情况下,原始的$softmax(\tau = 1.0)$ 并不能很好的区分不同输入之间的差距(输出接近)。但是加上温度系数之后, 原始微小的输入差距会被放大。 这就是为什么$\tau$越小,模型越关注于将那些与本样本最相似的负样本分开。
-
原始$softmax$的梯度: $$ \begin{equation} \begin{aligned} \frac{\partial L}{\partial z_{i}} &= \sum_j\frac{\partial L}{\partial q_j}\frac{\partial q_j}{\partial z_i} \\ &=\frac{\exp(z_{i})}{\sum_{j}\exp(z_{j})}-y_{i} \end{aligned} \end{equation} $$
-
加了温度系数$\tau$之后$softmax$的梯度: $$ \begin{equation} \begin{aligned} \frac{\partial L}{\partial z_{i}} &= \sum_j\frac{\partial L}{\partial q_j}\frac{\partial q_j}{\partial z_i} \\ &=\frac{1}{\tau}\left(\frac{\exp(z_i/\tau)}{\sum_j\exp(z_j/\tau)}-y_i\right) \end{aligned} \end{equation} $$
对比损失对正样本的梯度: $$\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,i}}=-\frac1\tau\sum_{k\neq i}P_{i,k}$$
对负样本的梯度: $$\frac{\partial\mathcal{L}(x_i)}{\partial s_{i,j}}=\frac1\tau P_{i,j}$$
其中:$P_{i,j}=\frac{\exp(s_{i,j/}\tau)}{\sum_{k\neq i}\exp(s_{i,k}/\tau)+\exp(s_{i,i}/\tau)}$